---
title: "Excitation-Inhibition Balance Tuning"
subtitle: "Fitting Functional Connectivity Using FIC and EIB Algorithms"
format:
html:
code-fold: false
toc: true
echo: true
embed-resources: true
fig-width: 8
out-width: "100%"
jupyter: python3
execute:
cache: true
---
Try this notebook interactively:
[Download .ipynb](https://github.com/virtual-twin/tvboptim/blob/main/docs/workflows/EI_Tuning.ipynb){.btn .btn-primary download="EI_Tuning.ipynb"}
[Download .qmd](EI_Tuning.qmd){.btn .btn-secondary download="EI_Tuning.qmd"}
[Open in Colab](https://colab.research.google.com/github/virtual-twin/tvboptim/blob/main/docs/workflows/EI_Tuning.ipynb){.btn .btn-warning target="_blank"}
## Introduction
This tutorial demonstrates how to use TVB-Optim's Network Dynamics framework to implement **Excitation-Inhibition Balance (EIB) tuning** for whole-brain models, following the methodology introduced by [Schirner et al. (2023)](https://doi.org/10.1038/s41467-023-38626-y). The approach combines **Feedback Inhibition Control (FIC)** to locally maintain E-I balance with **EIB tuning** to globally optimize network connectivity patterns.
```{python}
#| output: false
#| echo: false
# Install dependencies if running in Google Colab
try:
import google.colab
print("Running in Google Colab - installing dependencies...")
!pip install -q tvboptim
print("✓ Dependencies installed!")
except ImportError:
pass # Not in Colab, assume dependencies are available
```
We'll use a two-population Reduced Wong-Wang model with separate excitatory and inhibitory populations, and optimize the network coupling to match empirical functional connectivity from resting-state fMRI. This biologically-inspired learning algorithm demonstrates how neural network parameters can be tuned to achieve desired functional connectivity while maintaining physiologically realistic dynamics.
**What this tutorial covers:**
- Two-population neural mass model with explicit E-I dynamics
- Dual coupling mechanism (long-range excitation and feedforward inhibition)
- Feedback Inhibition Control (FIC) to maintain target excitatory activity
- EIB tuning algorithm to match empirical functional connectivity
- BOLD signal simulation and FC computation
- Both iterative (Part 2) and gradient-based (Part 3) optimization approaches
**Reference:** Schirner, M., Deco, G., & Ritter, P. (2023). Learning how network structure shapes decision-making for bio-inspired computing. *Nature Communications*, *14*(1), Article 1. https://doi.org/10.1038/s41467-023-38626-y
```{python}
#| output: false
#| code-fold: true
#| code-summary: "Environment Setup and Imports"
#| echo: true
# Set up environment
import os
import time
cpu = True
if cpu:
N = 8
os.environ['XLA_FLAGS'] = f'--xla_force_host_platform_device_count={N}'
# Import all required libraries
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patheffects as path_effects
import jax
import jax.numpy as jnp
import copy
import optax
from scipy import io
import equinox as eqx
# Jax enable x64
jax.config.update("jax_enable_x64", True)
# Import from tvboptim
from tvboptim.types import Parameter, BoundedParameter
from tvboptim.types.stateutils import show_parameters
from tvboptim.utils import set_cache_path, cache
from tvboptim.optim.optax import OptaxOptimizer
from tvboptim.optim.callbacks import MultiCallback, DefaultPrintCallback, SavingLossCallback
# Network dynamics imports
from tvboptim.experimental.network_dynamics import Network, solve, prepare
from tvboptim.experimental.network_dynamics.dynamics.tvb import ReducedWongWang
from tvboptim.experimental.network_dynamics.coupling import LinearCoupling, FastLinearCoupling
from tvboptim.experimental.network_dynamics.graph import DenseDelayGraph, DenseGraph
from tvboptim.experimental.network_dynamics.solvers import Heun, BoundedSolver
from tvboptim.experimental.network_dynamics.noise import AdditiveNoise
from tvboptim.data import load_structural_connectivity, load_functional_connectivity
# BOLD monitoring
from tvboptim.observations.tvb_monitors.bold import Bold
# Observation functions
from tvboptim.observations.observation import compute_fc, fc_corr, rmse
# Caching utilities
from tvboptim.utils import set_cache_path, cache
# Set cache path for tvboptim
set_cache_path("./ei_tuning")
```
## Loading Structural Data and Target FC
We load the Desikan-Killiany parcellation structural connectivity and empirical functional connectivity from resting-state fMRI data.
```{python}
#| output: false
#| echo: true
#| code-fold: true
#| code-summary: "Load structural connectivity and target FC"
# Load structural connectivity with region labels
weights, lengths, region_labels = load_structural_connectivity(name="dk_average")
# Normalize weights to [0, 1] range
weights = weights / jnp.max(weights)
n_nodes = weights.shape[0]
# Delays
speed = 3.0
delays = lengths / speed
# Load empirical functional connectivity as optimization target
fc_target = load_functional_connectivity(name="dk_average")
```
```{python}
#| label: fig-data
#| fig-cap: "**Structural and functional connectivity data.** Left: Normalized structural connection weights. Middle: Fiber transmission delays (ms). Right: Target empirical functional connectivity from resting-state fMRI."
#| code-fold: true
#| code-summary: "Visualization code"
# Define consistent color palette derived from cividis
import matplotlib.colors as mcolors
cividis_cmap = plt.cm.cividis
cividis_colors = cividis_cmap(np.linspace(0, 1, 256))
accent_blue = cividis_cmap(0.3) # Dark blue from cividis
accent_gold = cividis_cmap(0.85) # Gold/yellow from cividis
accent_mid = cividis_cmap(0.6) # Mid-tone
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(8.1, 4))
# Structural weights - use cividis
im1 = ax1.imshow(weights, cmap='cividis', vmin=0, vmax=1)
ax1.set_title('Structural Weights')
ax1.set_xlabel('Region')
ax1.set_ylabel('Region')
plt.colorbar(im1, ax=ax1, fraction=0.046)
# Delays - use cividis
im2 = ax2.imshow(delays, cmap='cividis')
ax2.set_title('Transmission Delays (ms)')
ax2.set_xlabel('Region')
ax2.set_ylabel('Region')
plt.colorbar(im2, ax=ax2, fraction=0.046, label='ms')
# Target FC - use cividis
im3 = ax3.imshow(fc_target, vmin=0, vmax=1.0, cmap='cividis')
ax3.set_title('Target Functional Connectivity')
ax3.set_xlabel('Region')
ax3.set_ylabel('Region')
plt.colorbar(im3, ax=ax3, label='Correlation', fraction=0.046)
plt.tight_layout()
plt.show()
```
## Model Definitions
### Two-Population Reduced Wong-Wang Model
This model extends the standard Reduced Wong-Wang with explicit excitatory (E) and inhibitory (I) populations, each with separate synaptic gating variables (S_e, S_i) and transfer functions. This enables independent control of E-I balance via the J_i parameter.
```{python}
#| echo: true
#| code-fold: true
#| code-summary: "ReducedWongWangEIB implementation"
from typing import Tuple
from tvboptim.experimental.network_dynamics.dynamics.base import AbstractDynamics
from tvboptim.experimental.network_dynamics.core.bunch import Bunch
class ReducedWongWangEIB(AbstractDynamics):
"""Two-population Reduced Wong-Wang model with E-I balance support"""
STATE_NAMES = ('S_e', 'S_i')
INITIAL_STATE = (0.001, 0.001)
AUXILIARY_NAMES = ('H_e', 'H_i')
DEFAULT_PARAMS = Bunch(
# Excitatory population parameters
a_e=310.0, # Input gain parameter
b_e=125.0, # Input shift parameter [Hz]
d_e=0.160, # Input scaling parameter [s]
gamma_e=0.641/1000, # Kinetic parameter
tau_e=100.0, # NMDA decay time constant [ms]
w_p=1.4, # Excitatory recurrence weight
W_e=1.0, # External input scaling weight
# Inhibitory population parameters
a_i=615.0, # Input gain parameter
b_i=177.0, # Input shift parameter [Hz]
d_i=0.087, # Input scaling parameter [s]
gamma_i=1.0/1000, # Kinetic parameter
tau_i=10.0, # NMDA decay time constant [ms]
W_i=0.7, # External input scaling weight
# Synaptic weights
J_N=0.15, # NMDA current [nA]
J_i=1.0, # Inhibitory synaptic weight
# External inputs
I_o=0.382, # Background input current
I_ext=0.0, # External stimulation current
# Coupling parameters
lamda=1.0, # Lambda: inhibitory coupling scaling
)
COUPLING_INPUTS = {
'coupling': 2, # Long-range excitation and Feedforward inhibition
}
def dynamics(
self,
t: float,
state: jnp.ndarray,
params: Bunch,
coupling: Bunch,
external: Bunch
) -> Tuple[jnp.ndarray, jnp.ndarray]:
"""Compute two-population Wong-Wang dynamics with dual coupling."""
# Unpack state variables
S_e = state[0] # Excitatory synaptic gating
S_i = state[1] # Inhibitory synaptic gating
# Unpack coupling inputs
c_lre = params.J_N * coupling.coupling[0] # Long-range excitation
c_ffi = params.J_N * coupling.coupling[1] # Feedforward inhibition
# Excitatory population input
J_N_S_e = params.J_N * S_e
x_e_pre = (params.w_p * J_N_S_e - params.J_i * S_i +
params.W_e * params.I_o + c_lre + params.I_ext)
# Excitatory transfer function
x_e = params.a_e * x_e_pre - params.b_e
H_e = x_e / (1.0 - jnp.exp(-params.d_e * x_e))
# Excitatory dynamics
dS_e_dt = -(S_e / params.tau_e) + (1.0 - S_e) * H_e * params.gamma_e
# Inhibitory population input
x_i_pre = J_N_S_e - S_i + params.W_i * params.I_o + params.lamda * c_ffi
# Inhibitory transfer function
x_i = params.a_i * x_i_pre - params.b_i
H_i = x_i / (1.0 - jnp.exp(-params.d_i * x_i))
# Inhibitory dynamics
dS_i_dt = -(S_i / params.tau_i) + H_i * params.gamma_i
# Package results
derivatives = jnp.array([dS_e_dt, dS_i_dt])
auxiliaries = jnp.array([H_e, H_i])
return derivatives, auxiliaries
```
### Dual-Weight EIB Coupling
This coupling mechanism produces two outputs from incoming excitatory activity: long-range excitation (wLRE) and feedforward inhibition (wFFI). Separate weight matrices enable independent tuning of excitatory and inhibitory pathways.
```{python}
#| echo: true
#| code-fold: true
#| code-summary: "EIBLinearCoupling implementation"
from tvboptim.experimental.network_dynamics.coupling.base import InstantaneousCoupling
class EIBLinearCoupling(InstantaneousCoupling):
"""EIB Linear coupling with separate excitatory and inhibitory weight matrices.
This coupling produces two outputs:
c_lre: Long-range excitation (wLRE * S_e)
c_ffi: Feedforward inhibition (wFFI * S_e)
Both couplings are driven by the excitatory activity (S_e) from other regions.
"""
N_OUTPUT_STATES = 2 # Produces two coupling outputs
DEFAULT_PARAMS = Bunch(
wLRE = 1.0, # Long-range excitation weight matrix
wFFI = 1.0, # Feedforward inhibition weight matrix
)
def pre(
self,
incoming_states: jnp.ndarray,
local_states: jnp.ndarray,
params: Bunch
) -> jnp.ndarray:
"""Pre-synaptic transformation: multiply S_e with wLRE and wFFI."""
# incoming_states[0] is S_e from all source nodes
S_e = incoming_states[0] # [n_target, n_source]
# Apply weights: element-wise multiply S_e with each weight matrix
# params.wLRE and params.wFFI have shape [n_nodes, n_nodes]
c_lre = S_e * params.wLRE # [n_target, n_source]
c_ffi = S_e * params.wFFI # [n_target, n_source]
# Stack into [2, n_target, n_source]
return jnp.stack([c_lre, c_ffi], axis=0)
def post(
self,
summed_inputs: jnp.ndarray,
local_states: jnp.ndarray,
params: Bunch
) -> jnp.ndarray:
"""Post-synaptic transformation: pass through without scaling."""
return summed_inputs
```
## Building the Network Model
We combine the EIB dynamics with structural connectivity and initialize the dual weight matrices.
```{python}
#| echo: true
#| output: true
# Create network components
graph = DenseGraph(weights, region_labels=region_labels)
dynamics = ReducedWongWangEIB(J_i = jnp.ones((n_nodes)))
# Initialize EIB coupling with dual weight matrices
# wLRE and wFFI start as copies of structural connectivity
coupling = EIBLinearCoupling(incoming_states=["S_e"])
# Set the weight matrices to the proper shape based on structural connectivity
# Both start as scaled versions of structural connectivity
coupling.params.wLRE = jnp.ones((n_nodes, n_nodes)) #+ 0.8*fc_target # [n_nodes, n_nodes]
coupling.params.wFFI = jnp.ones((n_nodes, n_nodes)) #- 0.8*fc_target # [n_nodes, n_nodes]
# Small noise to break symmetry
noise = AdditiveNoise(sigma=0.01, apply_to="S_e")
# Assemble the network
network = Network(
dynamics=dynamics,
coupling={'coupling': coupling}, # Both use same coupling but produce different outputs
graph=graph,
noise=noise
)
print(f"Network created with {n_nodes} nodes")
```
## Initial Simulation
Before applying any tuning algorithms, we run an initial transient simulation to establish a baseline quasi-stationary state.
```{python}
#| echo: true
# Prepare simulation: compile model and initialize state
t1 = 5 * 60_000 # Simulation duration (ms) - 1 minute for initial transient
dt = 4.0 # Integration timestep (ms) matching original script
solver = BoundedSolver(Heun(), low=0.0, high=1.0)
model, state = prepare(network, solver, t1=t1, dt=dt)
# Run initial transient to reach quasi-stationary state
print("Running initial transient simulation...")
result_init = jax.block_until_ready(model(state))
# Update network with final state as new initial conditions
network.update_history(result_init)
# Prepare for shorter simulations used in EI tuning
bold_TR = 720.0
model_short, state_short = prepare(network, solver, t1=bold_TR, dt=dt)
print(f"Initial simulation complete. Final S_e mean: {result_init.data[-1, 0, :].mean():.3f}")
print(f"Initial simulation complete. Final S_i mean: {result_init.data[-1, 1, :].mean():.3f}")
```
## BOLD Signal Setup
We configure BOLD monitoring to convert neural activity into hemodynamic signals for FC computation.
```{python}
#| echo: true
# Create BOLD monitor - we'll monitor S_e (first state variable)
# The BOLD period is 720ms (TR) as in the original script
bold_monitor = Bold(
period=bold_TR, # BOLD sampling period (TR = 720 ms)
downsample_period=4.0, # Intermediate downsampling matches dt
voi=0, # Monitor first state variable (S_e)
history=result_init # Use initial state as warm start for BOLD history
)
print("BOLD monitor initialized")
```
## Utility Functions
We define shared evaluation functions used throughout the tutorial.
```{python}
#| echo: true
#| code-fold: true
#| code-summary: "Utility functions for FC evaluation"
# Will be populated after initial simulation completes
model_eval, state_eval, _state = None, None, None
def setup_eval_model():
"""Setup evaluation model for FC computation (called after initial simulation)."""
global model_eval, state_eval, _state
model_eval, state_eval = prepare(network, Heun(), t1=t1, dt=dt)
_state = copy.deepcopy(state_eval)
def eval_fc(J_i, wLRE, wFFI):
"""Evaluate FC for given parameters using a long simulation."""
_state.dynamics.J_i = J_i
_state.coupling.coupling.wLRE = wLRE
_state.coupling.coupling.wFFI = wFFI
# Run simulation
raw_result = model_eval(_state)
# Compute BOLD
bold_signal = bold_monitor(raw_result)
# Compute FC (skip initial transient)
fc = compute_fc(bold_signal, skip_t=20)
return fc
print("Utility functions defined")
```
## Part 1: Feedback Inhibition Control (FIC)
Neural mass models with explicit E-I populations face stability challenges: runaway excitation, complete silencing, or heterogeneous operating points across regions. FIC solves this by adaptively adjusting the local inhibitory weight **J_i** to maintain excitatory activity at a target level (~0.25).
The update rule measures mean activity and adjusts inhibition proportionally:
$$\Delta J_i = \eta_{FIC} \cdot (\langle S_i \rangle \langle S_e \rangle - r_{target} \langle S_i \rangle)$$
When $\langle S_e \rangle > r_{target}$, inhibition increases; when $\langle S_e \rangle < r_{target}$, it decreases.
```{python}
#| echo: true
def FIC_update_rule(J_i, raw_data, eta_fic=0.1, target_fic=0.25):
"""Update J_i using FIC algorithm to maintain E-I balance."""
# Compute mean activity over the simulation window
mean_S_i = jnp.mean(raw_data[:, 1], axis=0) # Mean S_i over time [n_nodes]
mean_S_e = jnp.mean(raw_data[:, 0], axis=0) # Mean S_e over time [n_nodes]
# FIC update rule: increase J_i if E activity is too high
# When mean_S_e > target_fic, d_J_i is positive, increasing inhibition
d_J_i = eta_fic * (mean_S_i * mean_S_e - target_fic * mean_S_i)
J_i_new = J_i + d_J_i
return J_i_new
print("FIC update function defined")
```
### Running FIC Tuning
Let's now apply FIC in a simple loop to see how it stabilizes the network dynamics. We'll run the simulation for multiple iterations, applying the FIC update rule after each step to gradually adjust J_i until excitatory activity converges to the target level.
```{python}
#| echo: true
#| output: false
# FIC tuning parameters
eta_fic = 0.5 # Learning rate for FIC
target_fic = 0.25 # Target excitatory activity level
n_fic_steps = 200 # Number of FIC iterations
@cache("fic_tuning", redo=False)
def run_fic_tuning():
"""Run FIC tuning loop with caching."""
# Create a copy of the short simulation state for FIC tuning
state_fic = copy.deepcopy(state_short)
bold_monitor_fic = copy.deepcopy(bold_monitor)
# Store initial state for comparison
raw_result_pre_fic = model_short(state_fic)
# Setup for tracking BOLD signal during FIC
history_accessor = lambda tree: tree.history
bold_signal_fic = []
mean_S_e_history = []
# Random key for noise updates
key = jax.random.key(42)
print("Starting FIC tuning...")
# FIC tuning loop
for i in range(n_fic_steps):
# Simulate one time step
raw_result = model_short(state_fic)
# Compute BOLD signal for this step
bold_result = bold_monitor_fic(raw_result)
bold_signal_fic.append(bold_result.ys[0, 0, :])
# Track mean excitatory activity
mean_S_e = jnp.mean(raw_result.data[:, 0, :])
mean_S_e_history.append(mean_S_e)
# Update BOLD monitor history for next iteration
new_history = jnp.roll(bold_monitor_fic.history, -raw_result.data.shape[0], axis=0)
new_history = new_history.at[-raw_result.data.shape[0]:, :, :].set(raw_result.data[:, 0:1, :])
bold_monitor_fic = eqx.tree_at(history_accessor, bold_monitor_fic, new_history)
# Update initial conditions for next iteration
state_fic.initial_state.dynamics = raw_result.data[-1]
# Update noise realization
key, subkey = jax.random.split(key, 2)
state_fic._internal.noise_samples = jax.random.normal(key=subkey, shape=state_fic._internal.noise_samples.shape)
# Apply FIC update rule
state_fic.dynamics.J_i = FIC_update_rule(state_fic.dynamics.J_i, raw_result.data, eta_fic=eta_fic, target_fic=target_fic)
if (i + 1) % 50 == 0:
print(f" Step {i+1}/{n_fic_steps}, Mean S_e: {mean_S_e:.4f}, Target: {target_fic:.4f}")
# Final simulation after FIC
raw_result_post_fic = model_short(state_fic)
# Convert lists to arrays
bold_signal_fic = jnp.array(bold_signal_fic)
mean_S_e_history = jnp.array(mean_S_e_history)
print(f"FIC tuning complete!")
print(f"Final mean S_e: {mean_S_e_history[-1]:.4f} (target: {target_fic:.4f})")
return {
'state_fic': state_fic,
'bold_monitor_fic': bold_monitor_fic,
'raw_result_pre_fic': raw_result_pre_fic,
'raw_result_post_fic': raw_result_post_fic,
'bold_signal_fic': bold_signal_fic,
'mean_S_e_history': mean_S_e_history
}
# Run FIC tuning (cached)
fic_results = run_fic_tuning()
state_fic = fic_results['state_fic']
bold_monitor_fic = fic_results['bold_monitor_fic']
raw_result_pre_fic = fic_results['raw_result_pre_fic']
raw_result_post_fic = fic_results['raw_result_post_fic']
bold_signal_fic = fic_results['bold_signal_fic']
mean_S_e_history = fic_results['mean_S_e_history']
```
### FIC Results
```{python}
#| label: fig-fic-results
#| fig-cap: "**FIC algorithm results.** Top row: Excitatory activity (S_e) before and after FIC tuning, with target level shown (dashed line). Bottom left: Convergence of mean S_e to target over iterations. Bottom right: Evolution of BOLD signal during FIC tuning showing stabilization."
#| code-fold: true
#| code-summary: "Visualization code"
fig = plt.figure(figsize=(8.1, 7))
gs = fig.add_gridspec(2, 2, hspace=0.3, wspace=0.3)
# Use cividis-derived colors for consistency
target_color = accent_gold
trace_color = accent_blue
convergence_color = accent_mid
# Top left: Pre-FIC timeseries
ax1 = fig.add_subplot(gs[0, 0])
ax1.plot(raw_result_pre_fic.data[:, 0, :], alpha=0.6, linewidth=0.8, color=trace_color)
ax1.axhline(target_fic, color=target_color, linestyle='--', linewidth=2, label=f'Target ({target_fic})')
ax1.set_xlabel('Time step')
ax1.set_ylabel('S_e (Excitatory activity)')
ax1.set_title('Before FIC')
ax1.set_ylim(0, 1)
ax1.legend()
ax1.grid(True, alpha=0.3)
# Top right: Post-FIC timeseries
ax2 = fig.add_subplot(gs[0, 1])
ax2.plot(raw_result_post_fic.data[:, 0, :], alpha=0.6, linewidth=0.8, color=trace_color)
ax2.axhline(target_fic, color=target_color, linestyle='--', linewidth=2, label=f'Target ({target_fic})')
ax2.set_xlabel('Time step')
ax2.set_ylabel('S_e (Excitatory activity)')
ax2.set_title('After FIC')
ax2.set_ylim(0, 1)
ax2.legend()
ax2.grid(True, alpha=0.3)
# Bottom left: Convergence
ax3 = fig.add_subplot(gs[1, 0])
ax3.plot(mean_S_e_history, linewidth=2, label='Mean S_e', color=accent_blue)
ax3.axhline(target_fic, color=target_color, linestyle='--', linewidth=2, label=f'Target ({target_fic})')
ax3.set_xlabel('FIC iteration')
ax3.set_ylabel('Mean S_e')
ax3.set_title('FIC Convergence')
ax3.legend()
ax3.grid(True, alpha=0.3)
# Bottom right: BOLD signal evolution with mean overlay
ax4 = fig.add_subplot(gs[1, 1])
# Plot all regions with light colors from cividis
n_regions = bold_signal_fic.shape[1]
colors_bold = cividis_cmap(np.linspace(0.2, 0.9, n_regions))
for i in range(n_regions):
ax4.plot(bold_signal_fic[:, i], alpha=0.3, linewidth=0.8, color=colors_bold[i])
# Overlay mean BOLD signal in darker color
mean_bold = np.mean(bold_signal_fic, axis=1)
ax4.plot(mean_bold, color=accent_blue, linewidth=2.5, label='Mean', alpha=0.9)
ax4.set_xlabel('BOLD time point (TR)')
ax4.set_ylabel('BOLD signal')
ax4.set_title('BOLD Signal Evolution (all regions + mean)')
ax4.legend()
ax4.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
## Part 2: Excitation-Inhibition Balance (EIB) Tuning
FIC establishes local E-I balance but doesn't control network-level functional connectivity. EIB extends this by adjusting the dual coupling weights (wLRE, wFFI) to match empirical FC patterns.
The update rules increase wLRE and decrease wFFI when FC is too low, and vice versa when FC is too high:
$$\Delta w_{LRE}^{ij} = \eta_{EIB} \cdot (FC_{target}^{ij} - FC_{pred}^{ij}) \cdot RMSE_i$$
$$\Delta w_{FFI}^{ij} = -\eta_{EIB} \cdot (FC_{target}^{ij} - FC_{pred}^{ij}) \cdot RMSE_i$$
The row-wise RMSE term weights updates by each region's overall FC error.
```{python}
#| echo: true
def EI_update_rule(wLRE, wFFI, fc_pred, fc_target, eta_eib=0.02):
"""Update wLRE and wFFI using EIB algorithm"""
# Compute FC difference (positive means FC is too low, need more coupling)
diff_FC = fc_target - fc_pred
# Compute row-wise RMSE to weight updates by overall error magnitude
rmse_FC = rmse(fc_target, fc_pred, axis=1)[:, None] # [n_nodes, 1]
# Update rules:
# - Increase wLRE when FC is too low (strengthen excitation)
# - Decrease wFFI when FC is too low (reduce inhibition)
# Note: opposite signs ensure coordinated adjustment
wLRE_new = jnp.clip(wLRE + eta_eib * diff_FC * rmse_FC, 0, None)
wFFI_new = jnp.clip(wFFI - eta_eib * diff_FC * rmse_FC, 0, None)
return wLRE_new, wFFI_new
print("EIB update function defined")
```
### Combined FIC+EIB Tuning
We now run both algorithms simultaneously: FIC maintains local balance at each iteration, while EIB adjusts coupling weights based on a sliding window of BOLD signal to match target FC.
```{python}
#| echo: true
#| output: false
# Combined FIC+EIB tuning parameters
eta_fic = 0.1 # FIC learning rate
eta_eib = 0.005 # EIB learning rate (smaller than FIC)
window_size = 150 # Number of BOLD TRs for FC calculation
n_eib_steps = 2000 # Total number of iterations
snapshot_interval = 50 # Collect snapshots every N iterations
@cache("eib_tuning", redo=False)
def run_eib_tuning():
"""Run combined FIC+EIB tuning loop with caching."""
# Initialize state for combined tuning
state_ei = copy.deepcopy(state_fic)
bold_monitor_ei = copy.deepcopy(bold_monitor_fic)
history_accessor = lambda tree: tree.history
# BOLD signal sliding window
bold_signal = bold_signal_fic[-window_size:].reshape((window_size, 1, n_nodes))
# Track metrics during tuning
fc_correlations = []
fc_rmse_values = []
# Random key for noise
key = jax.random.key(43)
# Store initial state for comparison
raw_result_pre_eib = model_short(state_ei)
# Data collection for animation
snapshots = {
'iterations': [],
'bold_signal': [],
'raw_timeseries': [],
'J_i': [],
'fc_pred': [],
'fc_corr': [],
'fc_rmse': [],
'wLRE': [],
'wFFI': [],
}
print("Starting combined FIC+EIB tuning...")
# Combined FIC+EIB tuning loop
for i in range(n_eib_steps):
# 1. Simulate neural dynamics for one BOLD period
raw_result = model_short(state_ei)
# 2. Compute BOLD signal
bold_result = bold_monitor_ei(raw_result)
# 3. Update BOLD signal sliding window (rolling buffer)
bold_signal = jnp.roll(bold_signal, -1, axis=0)
bold_signal = bold_signal.at[-1, 0, :].set(bold_result.ys[0, 0, :])
# 4. Update BOLD monitor history for hemodynamic state continuity
new_history = jnp.roll(bold_monitor_ei.history, -raw_result.data.shape[0], axis=0)
new_history = new_history.at[-raw_result.data.shape[0]:, :, :].set(raw_result.data[:, 0:1, :])
bold_monitor_ei = eqx.tree_at(history_accessor, bold_monitor_ei, new_history)
# 5. Update initial conditions for next simulation
state_ei.initial_state.dynamics = raw_result.data[-1]
# 6. Update noise realization
key, subkey = jax.random.split(key, 2)
state_ei._internal.noise_samples = jax.random.normal(key=subkey, shape=state_ei._internal.noise_samples.shape)
# 7. Apply FIC update (every iteration)
state_ei.dynamics.J_i = FIC_update_rule(
state_ei.dynamics.J_i,
raw_result.data,
eta_fic=eta_fic,
target_fic=target_fic
)
# 8. Apply EIB update
# Compute FC from BOLD signal window
fc_pred = compute_fc(bold_signal)
# Update wLRE and wFFI using EIB rule
wLRE_new, wFFI_new = EI_update_rule(
state_ei.coupling.coupling.wLRE,
state_ei.coupling.coupling.wFFI,
fc_pred,
fc_target,
eta_eib=((i+1)/n_eib_steps) * eta_eib
)
state_ei.coupling.coupling.wLRE = wLRE_new
state_ei.coupling.coupling.wFFI = wFFI_new
# Track FC quality metrics
fc_corr_val = fc_corr(fc_pred, fc_target)
fc_rmse_val = jnp.sqrt(jnp.mean((fc_pred - fc_target)**2))
fc_correlations.append(fc_corr_val)
fc_rmse_values.append(fc_rmse_val)
# Collect snapshots for animation every N iterations
if (i + 1) % snapshot_interval == 0:
snapshots['iterations'].append(i + 1)
snapshots['bold_signal'].append(np.array(bold_signal[:, 0, :])) # [window_size, n_nodes]
snapshots['raw_timeseries'].append(np.array(raw_result.data[:, 0, :])) # [time_steps, n_nodes]
snapshots['J_i'].append(np.array(state_ei.dynamics.J_i.flatten())) # [n_nodes]
snapshots['wLRE'].append(np.array(state_ei.coupling.coupling.wLRE)) # [n_nodes, n_nodes]
snapshots['wFFI'].append(np.array(state_ei.coupling.coupling.wFFI)) # [n_nodes, n_nodes]
snapshots['fc_pred'].append(np.array(fc_pred))
snapshots['fc_corr'].append(float(fc_corr_val))
snapshots['fc_rmse'].append(float(fc_rmse_val))
# Print progress
print(f" Step {i+1}/{n_eib_steps}, FC corr: {fc_corr_val:.4f}, FC RMSE: {fc_rmse_val:.4f}")
# Store final state for comparison
raw_result_post_eib = model_short(state_ei)
# Convert metrics to arrays
fc_correlations = jnp.array(fc_correlations)
fc_rmse_values = jnp.array(fc_rmse_values)
print("Combined FIC+EIB tuning complete!")
print(f"Collected {len(snapshots['iterations'])} snapshots for animation")
return {
'state_ei': state_ei,
'raw_result_pre_eib': raw_result_pre_eib,
'raw_result_post_eib': raw_result_post_eib,
'fc_correlations': fc_correlations,
'fc_rmse_values': fc_rmse_values,
'snapshots': snapshots
}
# Run EIB tuning (cached)
eib_results = run_eib_tuning()
state_ei = eib_results['state_ei']
raw_result_pre_eib = eib_results['raw_result_pre_eib']
raw_result_post_eib = eib_results['raw_result_post_eib']
fc_correlations = eib_results['fc_correlations']
fc_rmse_values = eib_results['fc_rmse_values']
snapshots = eib_results['snapshots']
```
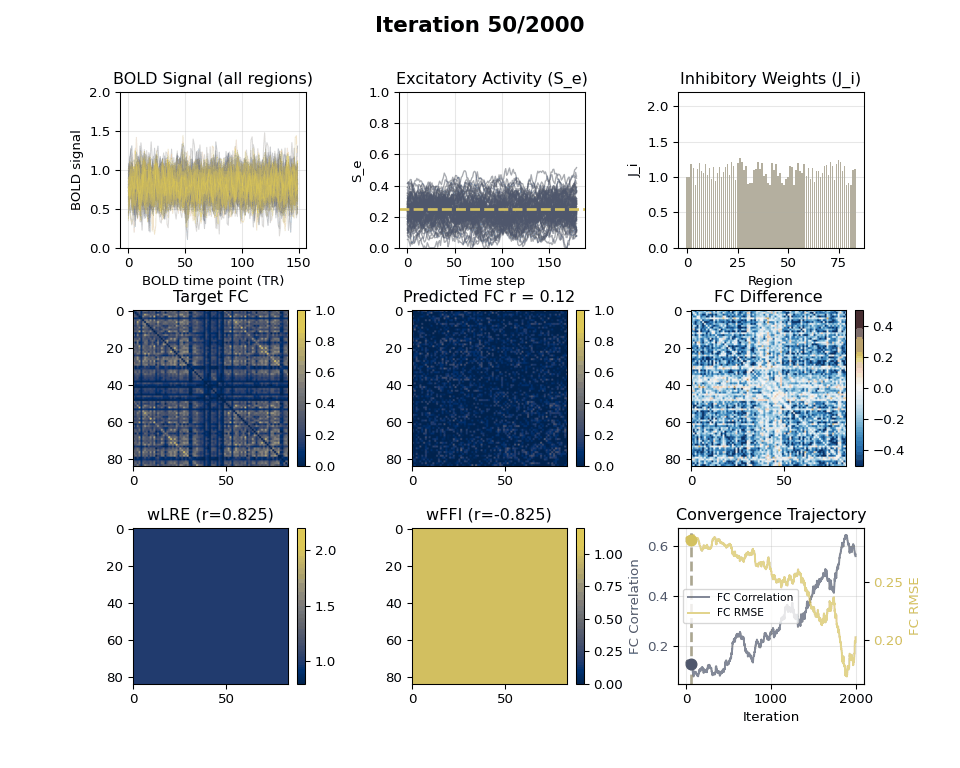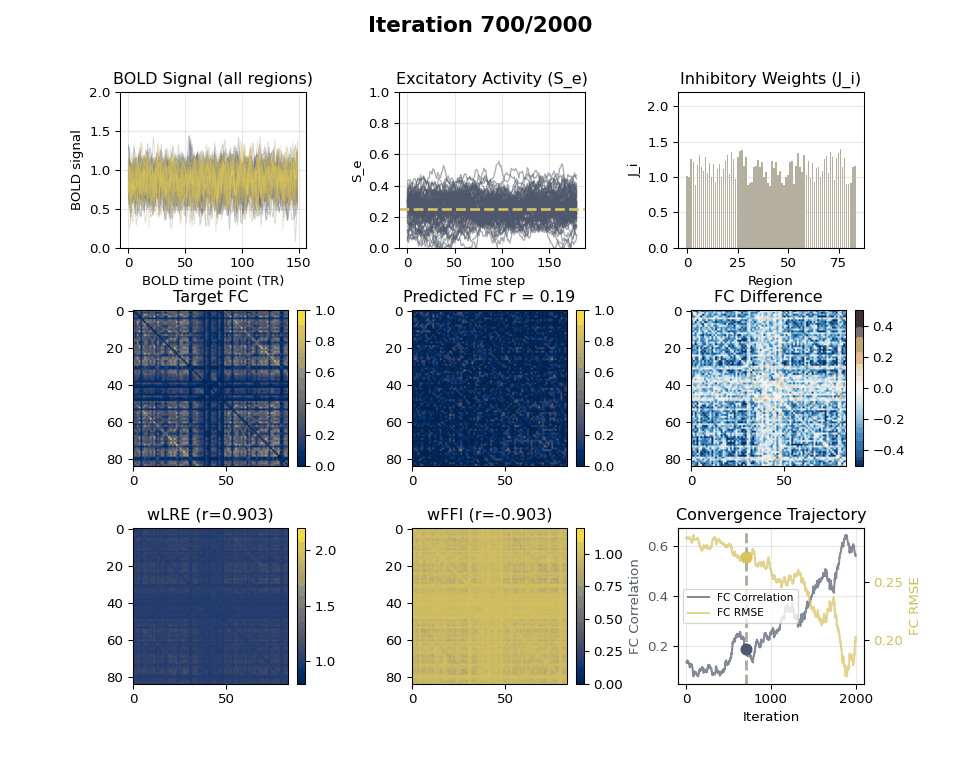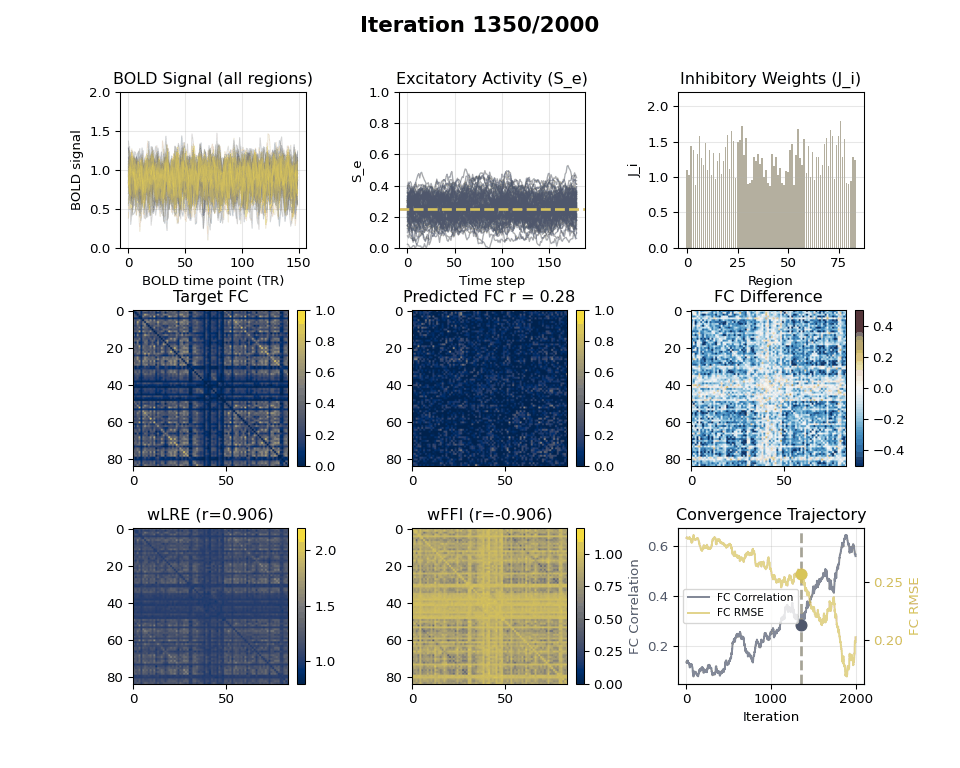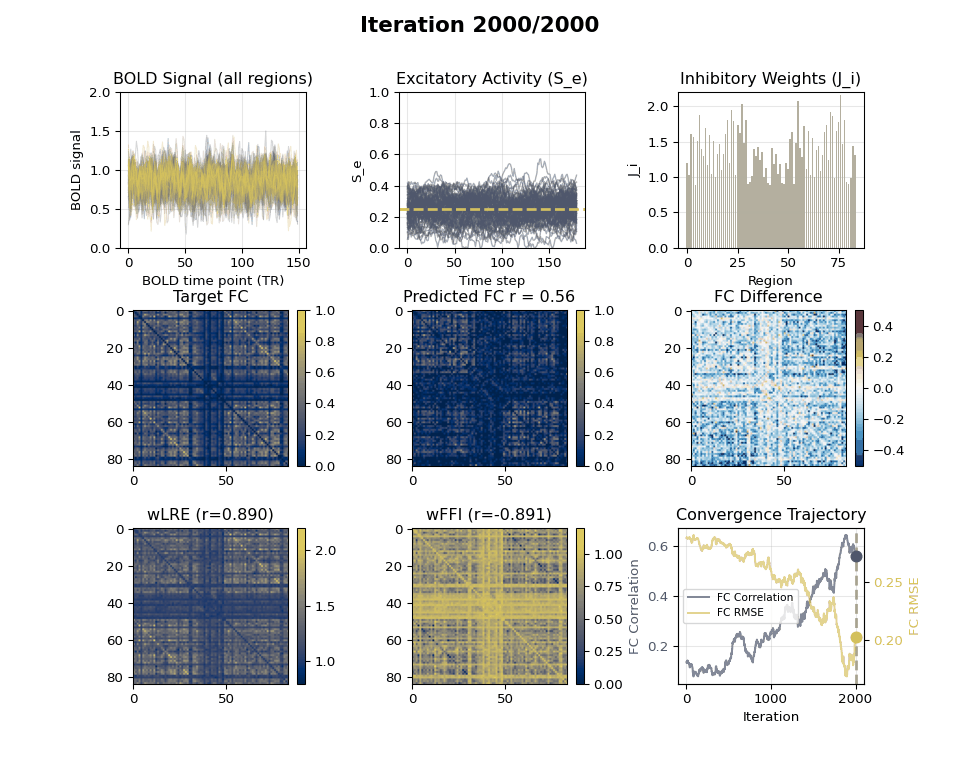
### Visualizing Tuning Progress: Animated GIF
Now we can create an animated GIF showing the tuning progression using the collected snapshots.
```{python}
#| echo: true
#| output: false
#| code-fold: true
#| code-summary: "Visualization code"
from matplotlib.animation import FuncAnimation, PillowWriter
import numpy as np
def create_animation_gif(output_path='ei_tuning_animation.gif', fps=2):
"""Create an animated GIF showing the tuning progression."""
fig = plt.figure(figsize=(10, 8), layout = "tight")
def update_frame(snapshot_idx):
"""Update function for animation."""
fig.clear()
gs = fig.add_gridspec(3, 3, hspace=0.4, wspace=0.5)
iteration = snapshots['iterations'][snapshot_idx]
bold_sig = snapshots['bold_signal'][snapshot_idx]
raw_ts = snapshots['raw_timeseries'][snapshot_idx]
J_i_vals = snapshots['J_i'][snapshot_idx]
wLRE_mat = snapshots['wLRE'][snapshot_idx]
wFFI_mat = snapshots['wFFI'][snapshot_idx]
fc_pred_mat = snapshots['fc_pred'][snapshot_idx]
fc_corr_val = snapshots['fc_corr'][snapshot_idx]
fc_rmse_val = snapshots['fc_rmse'][snapshot_idx]
# Define harmonized colors for animation
cividis_cmap = plt.cm.cividis
anim_blue = cividis_cmap(0.3)
anim_gold = cividis_cmap(0.85)
anim_mid = cividis_cmap(0.6)
# Row 1: BOLD signal and raw timeseries
ax1 = fig.add_subplot(gs[0, 0])
# Plot all BOLD traces with cividis colors
n_bold_regions = bold_sig.shape[1]
colors_anim_bold = cividis_cmap(np.linspace(0.2, 0.9, n_bold_regions))
for i in range(n_bold_regions):
ax1.plot(bold_sig[:, i], alpha=0.3, linewidth=0.8, color=colors_anim_bold[i])
ax1.set_xlabel('BOLD time point (TR)')
ax1.set_ylabel('BOLD signal')
ax1.set_title('BOLD Signal (all regions)')
ax1.grid(True, alpha=0.3)
ax1.set_ylim(0, 2)
ax2 = fig.add_subplot(gs[0, 1])
ax2.plot(raw_ts, alpha=0.5, linewidth=1, color=anim_blue)
ax2.axhline(target_fic, color=anim_gold, linestyle='--', linewidth=2)
ax2.set_xlabel('Time step')
ax2.set_ylabel('S_e')
ax2.set_title('Excitatory Activity (S_e)')
ax2.set_ylim(0, 1)
ax2.grid(True, alpha=0.3)
# Row 1, Col 3: J_i distribution
ax3 = fig.add_subplot(gs[0, 2])
ax3.bar(range(n_nodes), J_i_vals, alpha=0.7, color=anim_mid)
ax3.set_xlabel('Region')
ax3.set_ylabel('J_i')
ax3.set_title('Inhibitory Weights (J_i)')
ax3.grid(True, alpha=0.3, axis='y')
ax3.set_ylim(0, 2.2)
# Row 2: FC matrices - use cividis for FC, diverging for difference
ax4 = fig.add_subplot(gs[1, 0])
im4 = ax4.imshow(fc_target, vmin=0, vmax=1.0, cmap='cividis')
ax4.set_title('Target FC')
plt.colorbar(im4, ax=ax4, fraction=0.046)
ax5 = fig.add_subplot(gs[1, 1])
im5 = ax5.imshow(fc_pred_mat, vmin=0, vmax=1.0, cmap='cividis')
ax5.set_title(f'Predicted FC r = {fc_corr_val:.2f}')
plt.colorbar(im5, ax=ax5, fraction=0.046)
ax6 = fig.add_subplot(gs[1, 2])
fc_diff = fc_pred_mat - fc_target
im6 = ax6.imshow(fc_diff, vmin=-0.5, vmax=0.5, cmap='RdBu_r')
ax6.set_title('FC Difference')
plt.colorbar(im6, ax=ax6, fraction=0.046)
# Row 3: wLRE and wFFI matrices - use cividis
ax7 = fig.add_subplot(gs[2, 0])
im7 = ax7.imshow(wLRE_mat, vmin=0.8, vmax=2.2, cmap='cividis')
wLRE_corr = np.corrcoef(wLRE_mat.flatten(), fc_target.flatten())[0, 1]
ax7.set_title(f'wLRE (r={wLRE_corr:.3f})')
plt.colorbar(im7, ax=ax7, fraction=0.046)
ax8 = fig.add_subplot(gs[2, 1])
im8 = ax8.imshow(wFFI_mat, vmin=0, vmax=1.2, cmap='cividis')
wFFI_corr = np.corrcoef(wFFI_mat.flatten(), fc_target.flatten())[0, 1]
ax8.set_title(f'wFFI (r={wFFI_corr:.3f})')
plt.colorbar(im8, ax=ax8, fraction=0.046)
# Row 3, Col 3: Convergence trajectory with position marker
ax9 = fig.add_subplot(gs[2, 2])
ax9_twin = ax9.twinx()
# Plot full trajectories with harmonized colors
line1 = ax9.plot(fc_correlations, linewidth=1.5, alpha=0.7, color=anim_blue, label='FC Correlation')
line2 = ax9_twin.plot(fc_rmse_values, linewidth=1.5, alpha=0.7, color=anim_gold, label='FC RMSE')
# Add vertical line at current position
current_iter = snapshots['iterations'][snapshot_idx]
ax9.axvline(current_iter, color=anim_mid, linestyle='--', linewidth=2, alpha=0.8)
# Add marker at current position
ax9.plot(current_iter, fc_correlations[current_iter], 'o', color=anim_blue, markersize=8, zorder=5)
ax9_twin.plot(current_iter, fc_rmse_values[current_iter], 'o', color=anim_gold, markersize=8, zorder=5)
# Labels and styling
ax9.set_xlabel('Iteration')
ax9.set_ylabel('FC Correlation', color=anim_blue)
ax9.tick_params(axis='y', labelcolor=anim_blue)
ax9_twin.set_ylabel('FC RMSE', color=anim_gold)
ax9_twin.tick_params(axis='y', labelcolor=anim_gold)
ax9.set_title('Convergence Trajectory')
ax9.grid(True, alpha=0.3)
# Legend
lines = line1 + line2
labels = [l.get_label() for l in lines]
ax9.legend(lines, labels, loc='center left', fontsize=8)
fig.suptitle(f'Iteration {iteration}/{n_eib_steps}', fontsize=16, fontweight='bold')
# Create animation with last frame pause
# Create frame sequence with last frame repeated to make it pause longer
n_frames = len(snapshots['iterations'])
last_frame_repeats = 5 # Repeat last frame 5 times (2.5 seconds at 2 fps)
frame_sequence = list(range(n_frames)) + [n_frames - 1] * last_frame_repeats
anim = FuncAnimation(
fig,
update_frame,
frames=frame_sequence,
interval=1000/fps, # milliseconds between frames
repeat=True
)
# Save as GIF
writer = PillowWriter(fps=fps)
anim.save(output_path, writer=writer)
plt.close()
print(f"Animation saved to {output_path}")
return output_path
# Create the GIF (may take a minute depending on number of snapshots)
gif_path = create_animation_gif('ei_tuning_animation.gif', fps=2)
```
### EIB Results
```{python}
#| echo: true
#| output: false
#| code-fold: true
#| code-summary: "Evaluation code"
# Setup evaluation model
setup_eval_model()
# Compute FC before EIB (but after initial FIC from earlier)
print("Computing pre-EIB functional connectivity...")
fc_pre_eib = eval_fc(
state.dynamics.J_i,
state.coupling.coupling.wLRE,
state.coupling.coupling.wFFI
)
# Compute FC after combined FIC+EIB tuning
print("Computing post-EIB functional connectivity...")
fc_post_eib = eval_fc(
state_ei.dynamics.J_i,
state_ei.coupling.coupling.wLRE,
state_ei.coupling.coupling.wFFI
)
# Compute quality metrics
fc_corr_pre = fc_corr(fc_pre_eib, fc_target)
fc_corr_post = fc_corr(fc_post_eib, fc_target)
fc_rmse_pre = jnp.sqrt(jnp.mean((fc_pre_eib - fc_target)**2))
fc_rmse_post = jnp.sqrt(jnp.mean((fc_post_eib - fc_target)**2))
print(f"\nFC Quality Metrics:")
print(f" Pre-EIB - Correlation: {fc_corr_pre:.4f}, RMSE: {fc_rmse_pre:.4f}")
print(f" Post-EIB - Correlation: {fc_corr_post:.4f}, RMSE: {fc_rmse_post:.4f}")
print(f" Improvement: Δcorr = {fc_corr_post - fc_corr_pre:+.4f}, ΔRMSE = {fc_rmse_post - fc_rmse_pre:+.4f}")
```
```{python}
#| label: fig-eib-results
#| fig-cap: "**EIB tuning results.** Top row: Functional connectivity comparison showing target empirical FC (left), pre-EIB simulation (middle), and post-EIB simulation (right) with quality metrics. Bottom: Convergence trajectories showing FC correlation (blue, left axis) increasing and FC RMSE (gold, right axis) decreasing over iterations."
#| code-fold: true
#| code-summary: "Visualization code"
fig = plt.figure(figsize=(8.1, 4.63))
gs = fig.add_gridspec(2, 3, hspace=0.35, wspace=0.4, height_ratios=[1, 0.6])
# Top row: FC matrices - use cividis
ax1 = fig.add_subplot(gs[0, 0])
im1 = ax1.imshow(fc_target, vmin=0, vmax=1.0, cmap='cividis')
ax1.set_title('Target FC\n(Empirical)')
ax1.set_xlabel('Region')
ax1.set_ylabel('Region')
plt.colorbar(im1, ax=ax1, fraction=0.046)
ax2 = fig.add_subplot(gs[0, 1])
im2 = ax2.imshow(fc_pre_eib, vmin=0, vmax=1.0, cmap='cividis')
ax2.set_title(f'Pre-EIB FC\nCorr: {fc_corr_pre:.3f}, RMSE: {fc_rmse_pre:.3f}')
ax2.set_xlabel('Region')
plt.colorbar(im2, ax=ax2, fraction=0.046)
ax3 = fig.add_subplot(gs[0, 2])
im3 = ax3.imshow(fc_post_eib, vmin=0, vmax=1.0, cmap='cividis')
ax3.set_title(f'Post-EIB FC\nCorr: {fc_corr_post:.3f}, RMSE: {fc_rmse_post:.3f}')
ax3.set_xlabel('Region')
plt.colorbar(im3, ax=ax3, fraction=0.046)
# Bottom row: Dual-axis convergence plot spanning entire width
ax4 = fig.add_subplot(gs[1, :])
ax4_twin = ax4.twinx()
# Plot FC correlation on left axis
line1 = ax4.plot(fc_correlations, linewidth=2.5, color=accent_blue, label='FC Correlation')
ax4.set_xlabel('EIB iteration')
ax4.set_ylabel('FC Correlation with Target', color=accent_blue)
ax4.tick_params(axis='y', labelcolor=accent_blue)
ax4.set_xlim(0, len(fc_correlations))
ax4.grid(True, alpha=0.3)
# Plot FC RMSE on right axis
line2 = ax4_twin.plot(fc_rmse_values, linewidth=2.5, color=accent_gold, label='FC RMSE')
ax4_twin.set_ylabel('FC RMSE', color=accent_gold)
ax4_twin.tick_params(axis='y', labelcolor=accent_gold)
# Combined legend
lines = line1 + line2
labels = [l.get_label() for l in lines]
ax4.legend(lines, labels, loc='center left')
ax4.set_title('EIB Convergence')
plt.tight_layout()
plt.show()
```
::: {.callout-note}
This iterative implementation prioritizes clarity over performance. Python loops prevent JIT compilation, and manual state management adds overhead. Part 3 demonstrates a gradient-based alternative that achieves similar results with automatic differentiation.
:::
## Part 3: Gradient-Based Optimization Approach
Rather than manually designing update rules, we reformulate EI tuning as a differentiable optimization problem: define a loss function combining FC error and activity deviation, mark parameters as optimizable, and use JAX autodiff with modern optimizers. This provides automatic gradients, adaptive learning rates, and cleaner code.
The loss function combines FC RMSE with activity deviation from the FIC target:
```{python}
#| echo: true
#| output: false
#| code-fold: true
#| code-summary: "Setup and loss function"
# Prepare simulation
t1_opt = 5 * 60_000
dt_opt = 4.0
solver_opt = BoundedSolver(Heun(), low=0.0, high=1.0)
model_opt, state_opt = prepare(network, solver_opt, t1=t1_opt, dt=dt_opt)
# Create BOLD monitor
bold_monitor_opt = Bold(
period=bold_TR,
downsample_period=4.0,
voi=0,
history=result_init
)
print("Optimization model prepared")
```
```{python}
#| echo: true
#| output: true
def loss(state):
"""Combined loss function for FC matching and E-I balance"""
# Simulate neural dynamics
ts = model_opt(state)
# Compute BOLD signal from simulated activity
bold = bold_monitor_opt(ts)
# Loss component 1: FC discrepancy with empirical data
fc_pred = compute_fc(bold, skip_t=30) # Skip initial transient
fc_loss = rmse(fc_pred, fc_target)
# Loss component 2: Feedback inhibition control
# Penalize deviation from target excitatory activity level
mean_activity = jnp.mean(ts.data[-500:, 0, :], axis=0) # Mean S_e over final timesteps
activity_loss = jnp.mean((mean_activity - target_fic) ** 2)
# Combined loss (both terms have similar scales)
return fc_loss + activity_loss
# Evaluate initial loss
initial_loss = loss(state_opt)
print(f"Initial loss: {initial_loss:.4f}")
# Mark parameters for optimization (J_i, wLRE, wFFI) with appropriate constraints
state_opt.dynamics.J_i = Parameter(state_opt.dynamics.J_i)
state_opt.coupling.coupling.wLRE = BoundedParameter(jnp.ones((n_nodes, n_nodes)), low=0.0, high=jnp.inf)
state_opt.coupling.coupling.wFFI = BoundedParameter(jnp.ones((n_nodes, n_nodes)), low=0.0, high=jnp.inf)
```
```{python}
#| echo: true
#| output: true
@cache("gradient_optimization", redo=False)
def run_gradient_optimization():
"""Run gradient-based optimization with caching."""
# Create optimizer with AdaBelief algorithm
optimizer = OptaxOptimizer(
loss,
optax.adamaxw(learning_rate=0.033),
callback=MultiCallback([DefaultPrintCallback(), SavingLossCallback()])
)
# Run optimization for 50 steps
opt_state, opt_fitting_data = optimizer.run(state_opt, max_steps=66)
return opt_state, opt_fitting_data
# Run optimization (cached)
optimized_state, fitting_data = run_gradient_optimization()
```
```{python}
#| echo: true
#| output: true
#| code-fold: true
#| code-summary: "Evaluation and results"
# Evaluate optimized FC
print("Evaluating optimized functional connectivity...")
fc_opt = eval_fc(
optimized_state.dynamics.J_i,
optimized_state.coupling.coupling.wLRE,
optimized_state.coupling.coupling.wFFI
)
fc_corr_opt = fc_corr(fc_opt, fc_target)
fc_rmse_opt = rmse(fc_opt, fc_target)
print(f"\nOptimization Results:")
print(f" Pre-Optimization - Correlation: {fc_corr_pre:.4f}, RMSE: {fc_rmse_pre:.4f}")
print(f" Post-Optimization - Correlation: {fc_corr_opt:.4f}, RMSE: {fc_rmse_opt:.4f}")
print(f" Improvement: Δcorr = {fc_corr_opt - fc_corr_pre:+.4f}, ΔRMSE = {fc_rmse_opt - fc_rmse_pre:+.4f}")
```
```{python}
#| label: fig-gradient-results
#| fig-cap: "**Gradient-based optimization results.** Top left: Loss convergence trajectory. Top middle/right: Optimized coupling weight matrices (wFFI and wLRE). Bottom row: FC comparison showing target, pre-optimization, and post-optimization results with quality metrics."
#| code-fold: true
#| code-summary: "Visualization code"
# Extract loss values
loss_values = fitting_data["loss"].save
n_steps = len(loss_values)
fig = plt.figure(figsize=(8.1, 6))
gs = fig.add_gridspec(2, 3, hspace=0.3, wspace=0.4)
# Top left: Loss trajectory - use cividis-derived colors
ax1 = fig.add_subplot(gs[0, 0])
ax1.plot(loss_values, linewidth=2, color="k", alpha=0.9)
ax1.scatter(0, loss_values[0], s=80, color=accent_blue, zorder=5)
ax1.scatter(n_steps-1, loss_values.array[-1], s=80, color=accent_gold, zorder=5)
ax1.set_xlabel('Optimization Step')
ax1.set_ylabel('Combined Loss')
ax1.set_title('Loss Convergence')
ax1.grid(True, alpha=0.3)
# Top middle: wFFI matrix - use cividis
ax2 = fig.add_subplot(gs[0, 1])
im2 = ax2.imshow(optimized_state.coupling.coupling.wFFI, vmin=0, vmax=2, cmap='cividis')
ax2.set_title('Optimized wFFI')
ax2.set_xlabel('Source')
ax2.set_ylabel('Target')
plt.colorbar(im2, ax=ax2, fraction=0.046)
# Top right: wLRE matrix - use cividis
ax3 = fig.add_subplot(gs[0, 2])
im3 = ax3.imshow(optimized_state.coupling.coupling.wLRE, vmin=0, vmax=2, cmap='cividis')
ax3.set_title('Optimized wLRE')
ax3.set_xlabel('Source')
ax3.set_ylabel('Target')
plt.colorbar(im3, ax=ax3, fraction=0.046)
# Bottom row: FC comparison - use cividis
ax4 = fig.add_subplot(gs[1, 0])
im4 = ax4.imshow(fc_target, vmin=0, vmax=1.0, cmap='cividis')
ax4.set_title('Target FC')
plt.colorbar(im4, ax=ax4, fraction=0.046)
ax5 = fig.add_subplot(gs[1, 1])
im5 = ax5.imshow(fc_pre_eib, vmin=0, vmax=1.0, cmap='cividis')
ax5.set_title(f'Pre-Opt FC\nCorr: {fc_corr_pre:.3f}')
plt.colorbar(im5, ax=ax5, fraction=0.046)
ax6 = fig.add_subplot(gs[1, 2])
im6 = ax6.imshow(fc_opt, vmin=0, vmax=1.0, cmap='cividis')
ax6.set_title(f'Post-Opt FC\nCorr: {fc_corr_opt:.3f}')
plt.colorbar(im6, ax=ax6, fraction=0.046)
plt.show()
```