---
title: "TVB-Optim"
subtitle: "[JAX](https://jax.readthedocs.io/en/latest/)-based framework for brain network simulation and gradient-based optimization."
format:
html:
code-fold: false
toc: true
echo: true
fig-width: 8
out-width: "100%"
jupyter: python3
execute:
cache: true
---
{fig-align="center" width=60%}
## Key Features
- **Gradient-based optimization** - Fit thousands of parameters using automatic differentiation through the entire simulation pipeline
- **Performance** - JAX-powered with seamless GPU/TPU scaling
- **Flexible & extensible** - Build models with [Network Dynamics](./network_dynamics/network_dynamics.qmd), a composable framework for whole-brain modeling. Existing TVB workflows supported via [TVB-O](https://github.com/virtual-twin/tvbo).
- **Intuitive parameter control** - Mark values for optimization as [Parameter()](./basics/parameters_and_optimization.qmd). Define exploration spaces with [Axes](./basics/axes_and_spaces.qmd) for automatic parallel evaluation via JAX vmap/pmap.
## Installation
**Requires Python 3.11 or above**
::: {.panel-tabset}
## UV
```bash
uv pip install tvboptim
```
For development:
```bash
git clone https://github.com/virtual-twin/tvboptim.git
cd tvboptim
uv pip install -e ".[dev]"
```
## pip
```bash
pip install tvboptim
```
For development:
```bash
git clone https://github.com/virtual-twin/tvboptim.git
cd tvboptim
pip install -e ".[dev]"
```
:::
## Example: Optimizing Functional Connectivity of a Whole-Brain Network Model
```{python}
#| code-fold: true
#| code-summary: "Imports"
#| output: false
import jax
import jax.numpy as jnp
from tvboptim.experimental.network_dynamics import Network, solve, prepare
from tvboptim.experimental.network_dynamics.dynamics.tvb import ReducedWongWang
from tvboptim.experimental.network_dynamics.coupling import LinearCoupling, DelayedLinearCoupling
from tvboptim.experimental.network_dynamics.graph import DenseDelayGraph
from tvboptim.experimental.network_dynamics.noise import AdditiveNoise
from tvboptim.experimental.network_dynamics.solvers import Heun, BoundedSolver
from tvboptim.observations.tvb_monitors import Bold, SubSampling
from tvboptim.observations import compute_fc, fc_corr, rmse
from tvboptim.data import load_structural_connectivity, load_functional_connectivity
from tvboptim.types import Parameter
from tvboptim.optim import OptaxOptimizer
from tvboptim.optim.callbacks import DefaultPrintCallback, PrintParameterCallback
import optax
# Load example connectivity data (Desikan-Killiany 84-region parcellation)
# Structural connectivity: white matter connections derived from diffusion MRI
weights, lengths, labels = load_structural_connectivity("dk_average")
weights = weights / jnp.max(weights) # Normalize connection weights
delays = lengths / 3.0 # Convert tract lengths (mm) to delays (ms) at 3 m/s conduction velocity
# Functional connectivity: empirical correlation patterns from resting-state fMRI
target_fc = load_functional_connectivity("dk_average")
```
**Goal:** Fit a whole-brain network model (84 regions, Reduced Wong-Wang dynamics) to empirical fMRI functional connectivity by optimizing global coupling strength. The entire workflow takes just a few lines of code:
```{python}
# Build a brain network model with 84 regions
network = Network(
dynamics=ReducedWongWang(), # Neural mass model (local dynamics)
coupling={'delayed': DelayedLinearCoupling( # How regions communicate
incoming_states="S", G=0.5)},
graph=DenseDelayGraph(weights, delays, # Structural connectivity + delays
region_labels=labels),
noise=AdditiveNoise(sigma=0.01, # Stochastic fluctuations
key=jax.random.key(42))
)
# Run 60-second simulation (1 ms time steps)
solver = BoundedSolver(Heun(), low = 0.0, high = 1.0) # Keep S between 0 and 1
result = solve(network, solver, t0=0.0, t1=60_000.0, dt=1.0)
```
```{python}
#| code-fold: true
#| code-summary: "Visualize simulation result"
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10, 3))
# Get n colors from the viridis colormap
n = 10
colors = plt.cm.cividis_r(jnp.mean(result.ys[0:5000, 0, 0:n], axis = 0))
for i, color in enumerate(colors):
ax.plot(result.ts[0:5000], result.ys[0:5000, 0, i],
linewidth=0.8, alpha=0.9, color=color)
ax.set_xlabel('Time (ms)')
ax.set_ylabel('S (activity)')
ax.set_title(f'Neural activity trajectories ({n} example regions)')
plt.tight_layout()
plt.show()
```
**Next:** optimize coupling strength `G` to match empirical functional connectivity patterns. TVB-Optim uses automatic differentiation to compute gradients through the entire pipeline (dynamics → BOLD → FC), enabling efficient parameter tuning.
```{python}
#| eval: True
# Optimization workflow: fit coupling strength to match empirical functional connectivity
# Step 1: Prepare for optimization by converting the network to pure function + parameters
network.update_history(result) # Use simulation result to initialize delay history
simulator, params = prepare(network, solver, t0=0.0, t1=60_000.0, dt=1.0)
# Step 2: Set up BOLD fMRI monitor
# Converts neural activity to BOLD signal via Balloon-Windkessel hemodynamic model
# Sampled every 720 ms (≈1.4 Hz) to match typical fMRI temporal resolution
bold_monitor = Bold(history=result, period=720.0, downsample=SubSampling(period=4.0))
# Step 3: Mark parameter for optimization
params.coupling.delayed.G = Parameter(0.5)
# Compute initial FC for comparison
def get_fc(params):
"""Helper to compute FC from simulation."""
solution = simulator(params)
bold = bold_monitor(solution)
return compute_fc(bold)
fc_initial = get_fc(params)
# Step 4: Define loss and optimize
def loss(params):
"""Loss function using RMSE between predicted and empirical FC."""
predicted_fc = get_fc(params)
return rmse(predicted_fc, target_fc)
# Run optimization with Adam optimizer
opt = OptaxOptimizer(loss, optax.adam(learning_rate=0.03), callback=DefaultPrintCallback())
final_params, history = opt.run(params, max_steps=5)
# Compute final FC and print results
fc_final = get_fc(final_params)
print(f"\nOptimization complete: G={final_params.coupling.delayed.G:.3f}")
```
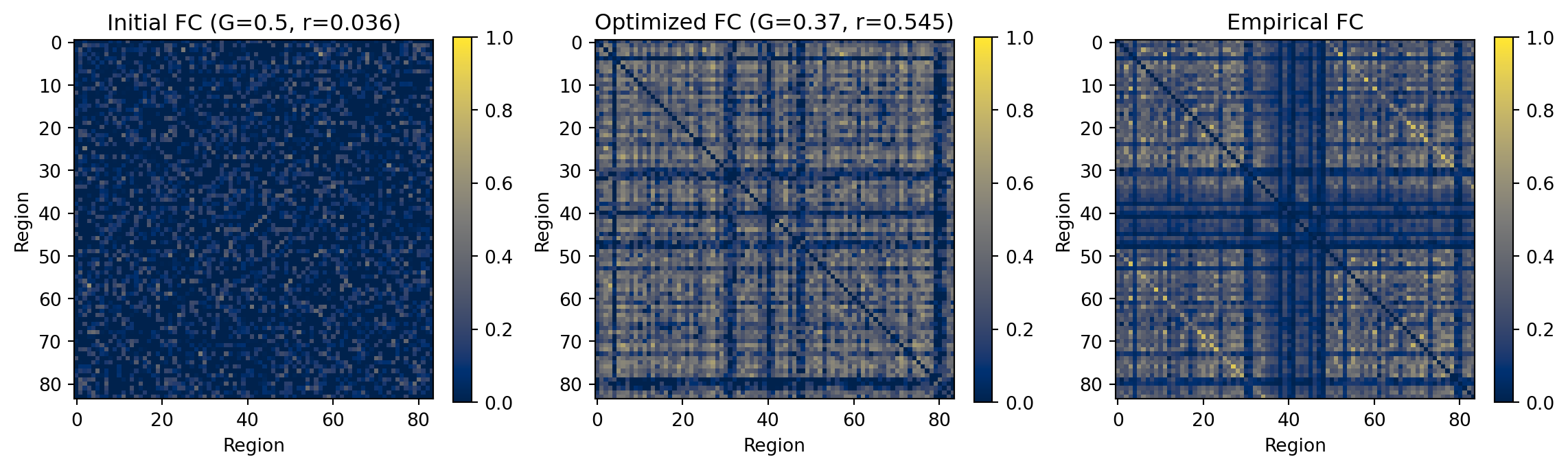
```{python}
#| code-fold: true
#| eval: True
#| code-summary: "Compare initial and optimized FC"
# Compute correlations
corr_initial = fc_corr(fc_initial, target_fc)
corr_final = fc_corr(fc_final, target_fc)
fig, axes = plt.subplots(1, 3, figsize=(12, 3.5))
# Initial FC
im0 = axes[0].imshow(fc_initial, cmap='cividis', vmin=0, vmax=1)
axes[0].set_title(f'Initial FC (G=0.5, r={corr_initial:.3f})')
axes[0].set_xlabel('Region')
axes[0].set_ylabel('Region')
plt.colorbar(im0, ax=axes[0], fraction=0.046)
# Final FC
im1 = axes[1].imshow(fc_final, cmap='cividis', vmin=0, vmax=1)
axes[1].set_title(f'Optimized FC (G={final_params.coupling.delayed.G:.2f}, r={corr_final:.3f})')
axes[1].set_xlabel('Region')
axes[1].set_ylabel('Region')
plt.colorbar(im1, ax=axes[1], fraction=0.046)
# Target FC
im2 = axes[2].imshow(target_fc, cmap='cividis', vmin=0, vmax=1)
axes[2].set_title('Empirical FC')
axes[2].set_xlabel('Region')
axes[2].set_ylabel('Region')
plt.colorbar(im2, ax=axes[2], fraction=0.046)
plt.tight_layout()
plt.show()
# Print correlation improvements
print(f"FC correlation improvement: {corr_initial:.3f} → {corr_final:.3f}")
```
**Result:** Gradient-based optimization successfully improved FC match. This approach scales to high-dimensional problems—multiple parameters, heterogeneous regional dynamics, or multi-condition fitting.
## Quickstart
The [Get Started](./basics/get_started.qmd) page provides an introduction to TVB-Optim with examples showing how to build models using Network Dynamics, [TVB-O](https://github.com/virtual-twin/tvbo), or by starting from existing TVB.
### Network Dynamics Framework
For direct model specification and optimization workflows:
- [Network Dynamics Introduction](./network_dynamics/network_dynamics.qmd) - Overview of the framework architecture
- [Complete Optimization Workflows](./network_dynamics/network_dynamics.qmd#complete-optimization-workflows) - End-to-end examples:
- [Reduced Wong-Wang BOLD FC Optimization](./workflows/RWW.qmd) - Fitting functional connectivity from fMRI
- [Jansen-Rit MEG Peak Frequency Gradient](./workflows/JR.qmd) - Reproducing spatial frequency patterns in MEG data
- [Excitation Inhibition Balance Tuning](./workflows/EI_Tuning.qmd) - Connectivity scale optimization with and without automatic differentiation
### Core Concepts
For advanced parameter handling and optimization techniques:
- [Parameters and Optimization](./basics/parameters_and_optimization.qmd) - Parameter types, spaces, and gradient-based optimization
- [Axes and Spaces](./basics/axes_and_spaces.qmd) - Systematic parameter exploration and heterogeneous configurations
### API Documentation
For detailed API reference, see the [Reference](reference/index.qmd) documentation.
## Development & Contributing
We welcome contributions and questions from the community!
- **Report Issues**: Found a bug or have a feature request? [Open an issue](https://github.com/virtual-twin/tvboptim/issues) on GitHub
- **Ask Questions**: Need help or have questions? [Start a discussion](https://github.com/virtual-twin/tvboptim/discussions)
- **Contribute Code**: Interested in contributing? Open a [pull request](https://github.com/virtual-twin/tvboptim/pulls) on GitHub
Copyright © 2025 Charité Universitätsmedizin Berlin