---
title: "Axes and Spaces: Systematic Parameter Exploration in TVB-Optim"
format:
html:
code-fold: false
toc: true
toc-depth: 3
fig-width: 8
out-width: "100%"
jupyter: python3
execute:
cache: true
---
# Introduction & Overview
The Axes and Spaces system in TVB-Optim provides a powerful, composable framework for systematic parameter exploration in brain network simulations. This system enables you to:
- **Define parameter sampling strategies** using different axis types
- **Compose complex parameter spaces** from multiple axes
- **Leverage JAX transformations** for efficient parallel execution
- **Seamlessly integrate** with optimization and analysis workflows
## Why This Design?
Traditional parameter exploration often requires writing custom loops and managing complex indexing. TVB-Optim's axis system provides a flexible and composable approach to make things easier.
Let's start with a quick preview of what we'll build:
```{python}
import jax
import jax.numpy as jnp
import numpy as np
import matplotlib.pyplot as plt
from tvboptim.types.spaces import Space, GridAxis, UniformAxis, DataAxis, NumPyroAxis
# Quick preview: A mixed parameter space
preview_state = {
'coupling_strength': GridAxis(0.0, 2.0, 4),
'noise_level': UniformAxis(0.01, 0.1, 3),
'fixed_param': 42.0
}
space = Space(preview_state, mode='product', key=jax.random.key(123))
print(f"Created parameter space with {len(space)} combinations")
# Show first few parameter combinations
for i, params in enumerate(space):
if i >= 5: break
print(f"Combination {i}: coupling={params['coupling_strength']:.2f}, "
f"noise={params['noise_level']:.4f}, fixed={params['fixed_param']}")
```
# Understanding Axes
## The AbstractAxis Interface
All axes in TVB-Optim implement a simple but powerful interface:
- **`generate_values(key=None)`**: Produces sample values as JAX arrays
- **`size`**: Returns the number of samples this axis generates
```{python}
# Let's examine the interface
from tvboptim.types.spaces import GridAxis
grid = GridAxis(0.0, 1.0, 5)
print(f"Axis size: {grid.size}")
print(f"Generated values: {grid.generate_values()}")
print(f"Values shape: {grid.generate_values().shape}")
```
Each axis type can implement completely different sampling strategies while maintaining a consistent interface.
## GridAxis - Deterministic Sampling
GridAxis provides systematic, deterministic sampling across parameter ranges. Perfect for sensitivity analysis and systematic exploration.
```{python}
# Basic grid sampling
grid_basic = GridAxis(0.0, 2.0, 11)
values_basic = grid_basic.generate_values()
print(f"Grid values: {values_basic}")
print(f"Spacing is uniform: {jnp.allclose(jnp.diff(values_basic), jnp.diff(values_basic)[0])}")
# Multiple grid densities
densities = [5, 10, 20]
for n in densities:
grid = GridAxis(0.0, 1.0, n)
values = grid.generate_values()
print(f"n={n:2d}: {len(values)} values from {values[0]:.3f} to {values[-1]:.3f}")
```
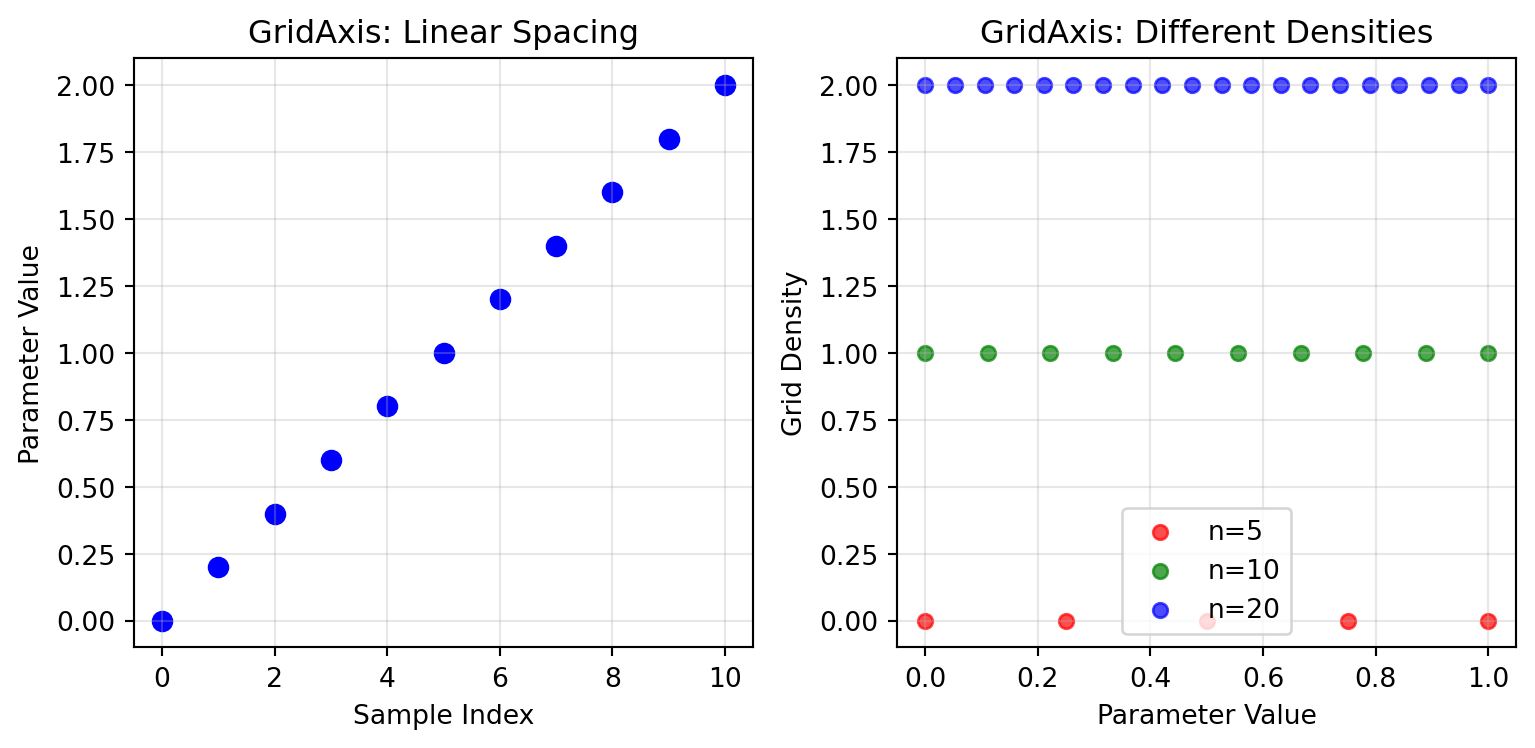
```{python}
#| code-fold: true
#| code-summary: "Show visualization code"
# Visualize grid sampling
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8.1, 4))
# Plot 1: Basic grid values
ax1.scatter(range(len(values_basic)), values_basic, color='blue', s=50)
ax1.set_xlabel('Sample Index')
ax1.set_ylabel('Parameter Value')
ax1.set_title('GridAxis: Linear Spacing')
ax1.grid(True, alpha=0.3)
# Plot 2: Multiple grid densities
colors = ['red', 'green', 'blue']
for i, (n, color) in enumerate(zip(densities, colors)):
grid = GridAxis(0.0, 1.0, n)
values = grid.generate_values()
ax2.scatter(values, [i] * len(values), color=color, s=30,
label=f'n={n}', alpha=0.7)
ax2.set_xlabel('Parameter Value')
ax2.set_ylabel('Grid Density')
ax2.set_title('GridAxis: Different Densities')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
### Shape Broadcasting with GridAxis
GridAxis supports shape broadcasting, which is useful for regional brain parameters in subsequent optimizations:
```{python}
# Example: Regional coupling strengths (68 brain regions)
n_regions = 68
regional_grid = GridAxis(0.0, 1.0, 5, shape=(n_regions,))
regional_values = regional_grid.generate_values()
print(f"Regional grid shape: {regional_values.shape}")
print(f"Each sample has shape: {regional_values[0].shape}")
print(f"Sample 2 value: {regional_values[2][0]:.3f} (broadcasted to all regions)")
print(f"All regions identical per sample: {jnp.allclose(regional_values[2], regional_values[2][0])}")
```
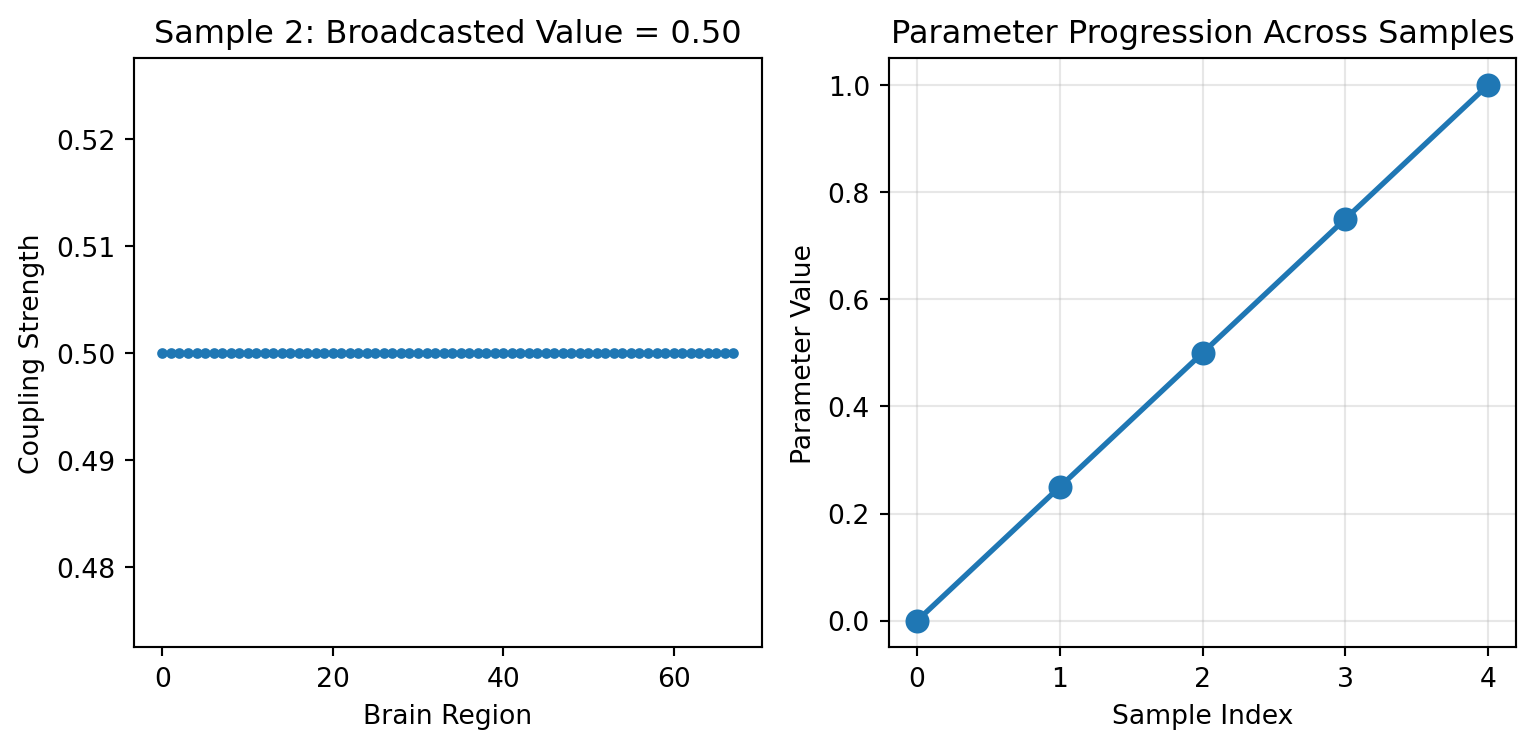
```{python}
#| code-fold: true
#| code-summary: "Show visualization code"
# Visualize the broadcasting
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8.1, 4))
# Show that each sample broadcasts the same value
sample_idx = 2
ax1.plot(regional_values[sample_idx], 'o-', markersize=3)
ax1.set_xlabel('Brain Region')
ax1.set_ylabel('Coupling Strength')
ax1.set_title(f'Sample {sample_idx}: Broadcasted Value = {regional_values[sample_idx][0]:.2f}')
# Show progression across samples
ax2.plot(range(5), regional_values[:, 0], 'o-', linewidth=2, markersize=8)
ax2.set_xlabel('Sample Index')
ax2.set_ylabel('Parameter Value')
ax2.set_title('Parameter Progression Across Samples')
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
## UniformAxis - Random Sampling
UniformAxis provides random sampling from uniform distributions, essential for more efficient stochastic exploration.
```{python}
# Reproducible random sampling
key = jax.random.key(42)
uniform = UniformAxis(0.0, 1.0, 100)
values1 = uniform.generate_values(key)
values2 = uniform.generate_values(key) # Same key = same values
values3 = uniform.generate_values(jax.random.key(43)) # Different key
print(f"Same key gives identical results: {jnp.allclose(values1, values2)}")
print(f"Different key gives different results: {not jnp.allclose(values1, values3)}")
print(f"Mean value: {jnp.mean(values1):.3f} (should be ~0.5)")
print(f"Value range: [{jnp.min(values1):.3f}, {jnp.max(values1):.3f}]")
```
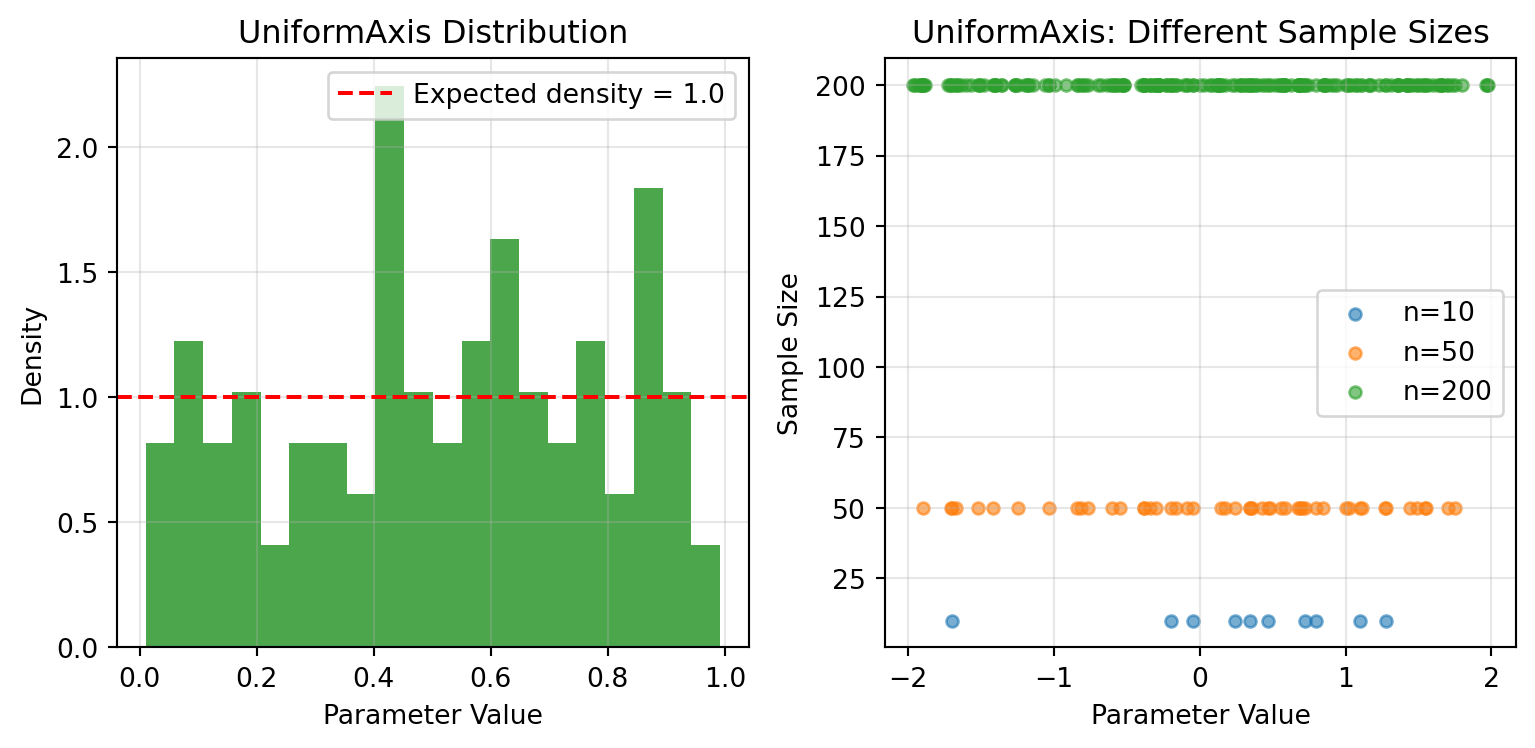
```{python}
#| code-fold: true
#| code-summary: "Show visualization code"
# Visualize distributions
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8.1, 4))
# Histogram of uniform samples
ax1.hist(values1, bins=20, alpha=0.7, color='green', density=True)
ax1.axhline(y=1.0, color='red', linestyle='--', label='Expected density = 1.0')
ax1.set_xlabel('Parameter Value')
ax1.set_ylabel('Density')
ax1.set_title('UniformAxis Distribution')
ax1.legend()
ax1.grid(True, alpha=0.3)
# Comparison of different sample sizes
sample_sizes = [10, 50, 200]
for size in sample_sizes:
uniform_temp = UniformAxis(-2.0, 2.0, size)
samples = uniform_temp.generate_values(jax.random.key(42))
ax2.scatter(samples, [size] * len(samples), alpha=0.6, s=20,
label=f'n={size}')
ax2.set_xlabel('Parameter Value')
ax2.set_ylabel('Sample Size')
ax2.set_title('UniformAxis: Different Sample Sizes')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
### Shape Broadcasting with UniformAxis
UniformAxis also supports shape broadcasting, useful for parameters that need the same random value across multiple dimensions:
```{python}
# Compare independent vs broadcast sampling
key = jax.random.key(123)
# Independent sampling: each element is different
uniform_independent = UniformAxis(0.0, 1.0, 3, shape=None)
independent_values = uniform_independent.generate_values(key)
# Broadcast sampling: same value across shape dimensions
uniform_broadcast = UniformAxis(0.0, 1.0, 3, shape=(4, 2))
broadcast_values = uniform_broadcast.generate_values(key)
print("Independent sampling:")
print(f"Shape: {independent_values.shape}")
print(f"Values: {independent_values}")
print("\nBroadcast sampling:")
print(f"Shape: {broadcast_values.shape}")
print("First sample (4x2 matrix):")
print(broadcast_values[0])
print(f"All values in first sample identical: {jnp.allclose(broadcast_values[0], broadcast_values[0].flatten()[0])}")
```
## DataAxis - Predefined Values
DataAxis lets you use predefined sequences of values.
```{python}
# Example: Testing specific coupling values from literature
literature_values = jnp.array([0.142, 0.284, 0.426, 0.568, 0.710])
data_axis = DataAxis(literature_values)
print(f"DataAxis size: {data_axis.size}")
print(f"Values: {data_axis.generate_values()}")
# Works with multidimensional data too
connectivity_matrices = jnp.array([
[[1.0, 0.5], [0.5, 1.0]], # Weak coupling
[[1.0, 0.8], [0.8, 1.0]], # Medium coupling
[[1.0, 1.2], [1.2, 1.0]] # Strong coupling
])
matrix_axis = DataAxis(connectivity_matrices)
print(f"\nMatrix axis shape: {matrix_axis.generate_values().shape}")
print("First connectivity matrix:")
print(matrix_axis.generate_values()[0])
# Create some creative data patterns
fib_values = jnp.array([1, 1, 2, 3, 5, 8, 13, 21])
fib_normalized = fib_values / fib_values.max()
print(f"\nFibonacci sequence (normalized): {fib_normalized}")
# Oscillatory pattern
t = jnp.linspace(0, 4*jnp.pi, 20)
oscillatory = 0.5 + 0.3 * jnp.sin(t)
print(f"Oscillatory pattern range: [{jnp.min(oscillatory):.3f}, {jnp.max(oscillatory):.3f}]")
```
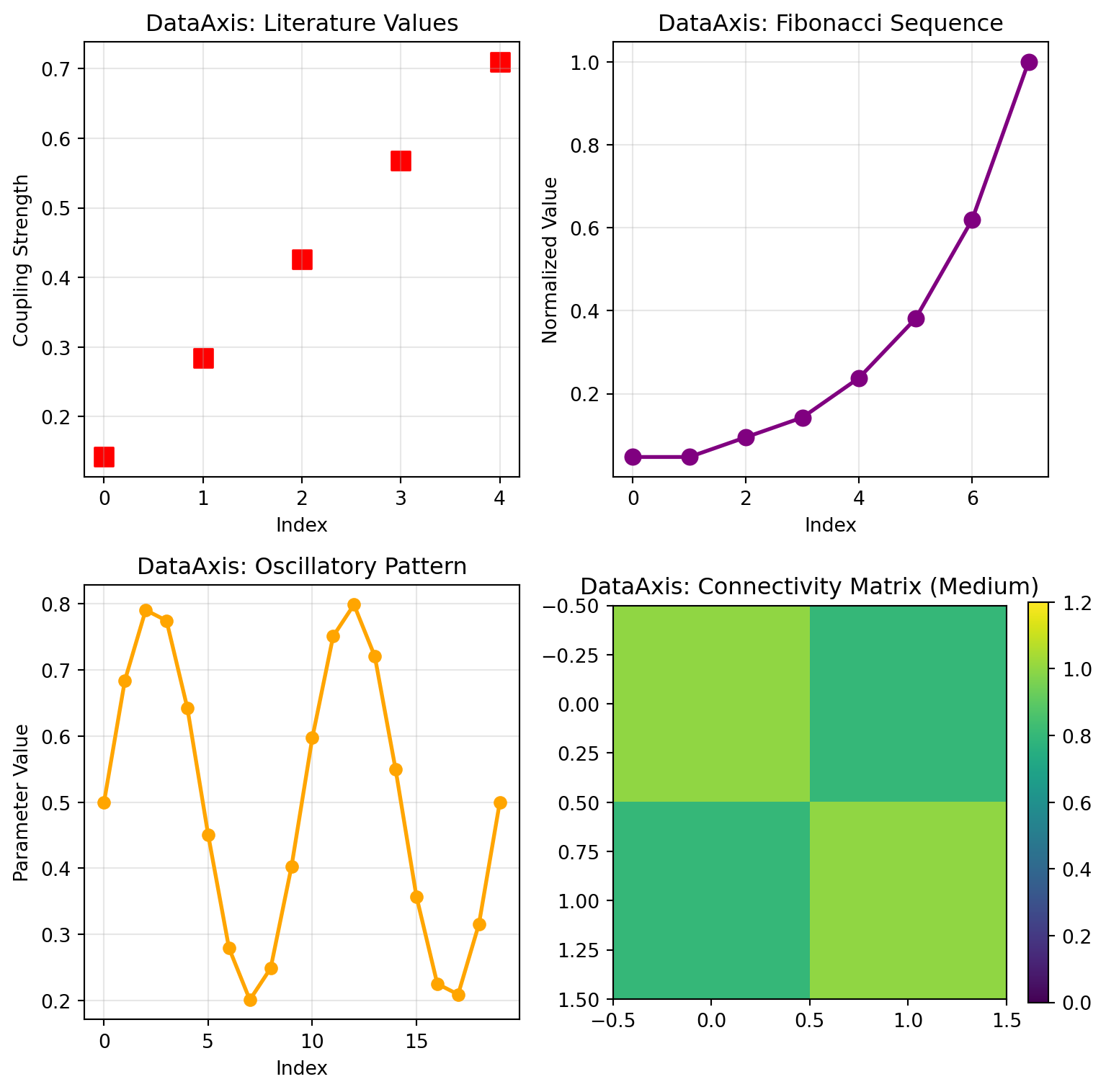
```{python}
#| code-fold: true
#| code-summary: "Show visualization code"
# Visualize different data patterns
fig, axes = plt.subplots(2, 2, figsize=(8.1, 8))
# 1. Literature values
ax = axes[0, 0]
ax.scatter(range(len(literature_values)), literature_values,
color='red', s=100, marker='s')
ax.set_xlabel('Index')
ax.set_ylabel('Coupling Strength')
ax.set_title('DataAxis: Literature Values')
ax.grid(True, alpha=0.3)
# 2. Fibonacci sequence
fib_axis = DataAxis(fib_normalized)
ax = axes[0, 1]
ax.plot(fib_normalized, 'o-', color='purple', linewidth=2, markersize=8)
ax.set_xlabel('Index')
ax.set_ylabel('Normalized Value')
ax.set_title('DataAxis: Fibonacci Sequence')
ax.grid(True, alpha=0.3)
# 3. Oscillatory pattern
osc_axis = DataAxis(oscillatory)
ax = axes[1, 0]
ax.plot(oscillatory, 'o-', color='orange', linewidth=2, markersize=6)
ax.set_xlabel('Index')
ax.set_ylabel('Parameter Value')
ax.set_title('DataAxis: Oscillatory Pattern')
ax.grid(True, alpha=0.3)
# 4. Connectivity matrix visualization
ax = axes[1, 1]
im = ax.imshow(matrix_axis.generate_values()[1], cmap='viridis', vmin=0, vmax=1.2)
ax.set_title('DataAxis: Connectivity Matrix (Medium)')
plt.colorbar(im, ax=ax, fraction=0.046)
plt.tight_layout()
plt.show()
```
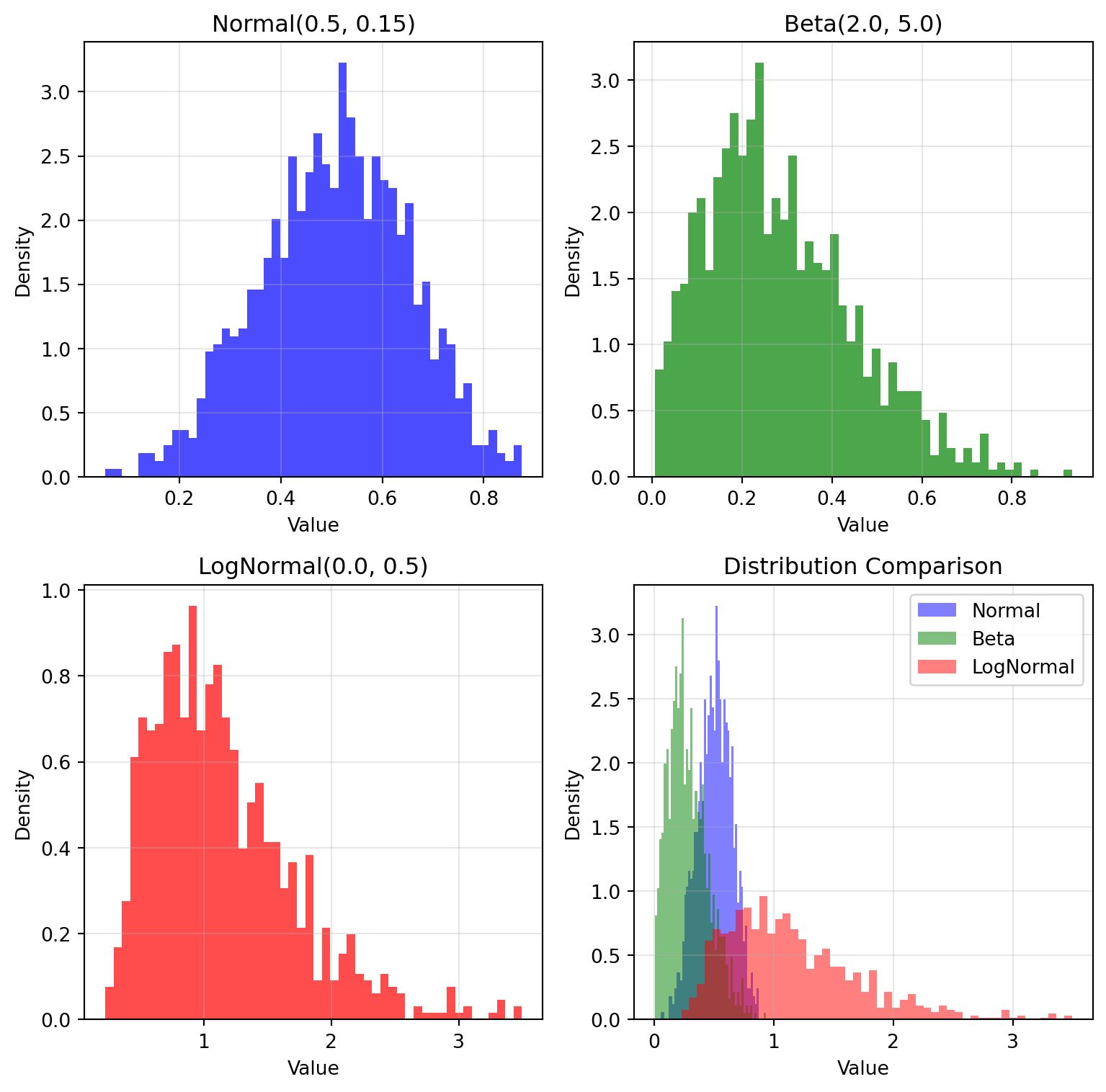
## NumPyroAxis - Distribution Sampling
NumPyroAxis brings the full power of probability distributions to parameter exploration, enabling sophisticated uncertainty quantification and Bayesian workflows.
```{python}
import numpyro.distributions as dist
# Different distribution types
key = jax.random.key(42)
# Normal distribution - common for many biological parameters
normal_axis = NumPyroAxis(dist.Normal(0.5, 0.15), n=1000)
normal_samples = normal_axis.generate_values(key)
# Beta distribution - great for bounded parameters [0,1]
beta_axis = NumPyroAxis(dist.Beta(2.0, 5.0), n=1000)
beta_samples = beta_axis.generate_values(key)
# LogNormal - for positive-only parameters like time constants
lognormal_axis = NumPyroAxis(dist.LogNormal(0.0, 0.5), n=1000)
lognormal_samples = lognormal_axis.generate_values(key)
print(f"Normal samples: mean={jnp.mean(normal_samples):.3f}, std={jnp.std(normal_samples):.3f}")
print(f"Beta samples: mean={jnp.mean(beta_samples):.3f}, range=[{jnp.min(beta_samples):.3f}, {jnp.max(beta_samples):.3f}]")
print(f"LogNormal samples: mean={jnp.mean(lognormal_samples):.3f}, median={jnp.median(lognormal_samples):.3f}")
```
```{python}
#| code-fold: true
#| code-summary: "Show visualization code"
# Visualize the distributions
fig, axes = plt.subplots(2, 2, figsize=(8.1, 8))
# Normal distribution
ax = axes[0, 0]
ax.hist(normal_samples, bins=50, density=True, alpha=0.7, color='blue')
ax.set_xlabel('Value')
ax.set_ylabel('Density')
ax.set_title('Normal(0.5, 0.15)')
ax.grid(True, alpha=0.3)
# Beta distribution
ax = axes[0, 1]
ax.hist(beta_samples, bins=50, density=True, alpha=0.7, color='green')
ax.set_xlabel('Value')
ax.set_ylabel('Density')
ax.set_title('Beta(2.0, 5.0)')
ax.grid(True, alpha=0.3)
# LogNormal distribution
ax = axes[1, 0]
ax.hist(lognormal_samples, bins=50, density=True, alpha=0.7, color='red')
ax.set_xlabel('Value')
ax.set_ylabel('Density')
ax.set_title('LogNormal(0.0, 0.5)')
ax.grid(True, alpha=0.3)
# Comparison of all three
ax = axes[1, 1]
ax.hist(normal_samples, bins=50, density=True, alpha=0.5, color='blue', label='Normal')
ax.hist(beta_samples, bins=50, density=True, alpha=0.5, color='green', label='Beta')
ax.hist(lognormal_samples[lognormal_samples < 5], bins=50, density=True, alpha=0.5, color='red', label='LogNormal')
ax.set_xlabel('Value')
ax.set_ylabel('Density')
ax.set_title('Distribution Comparison')
ax.legend()
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
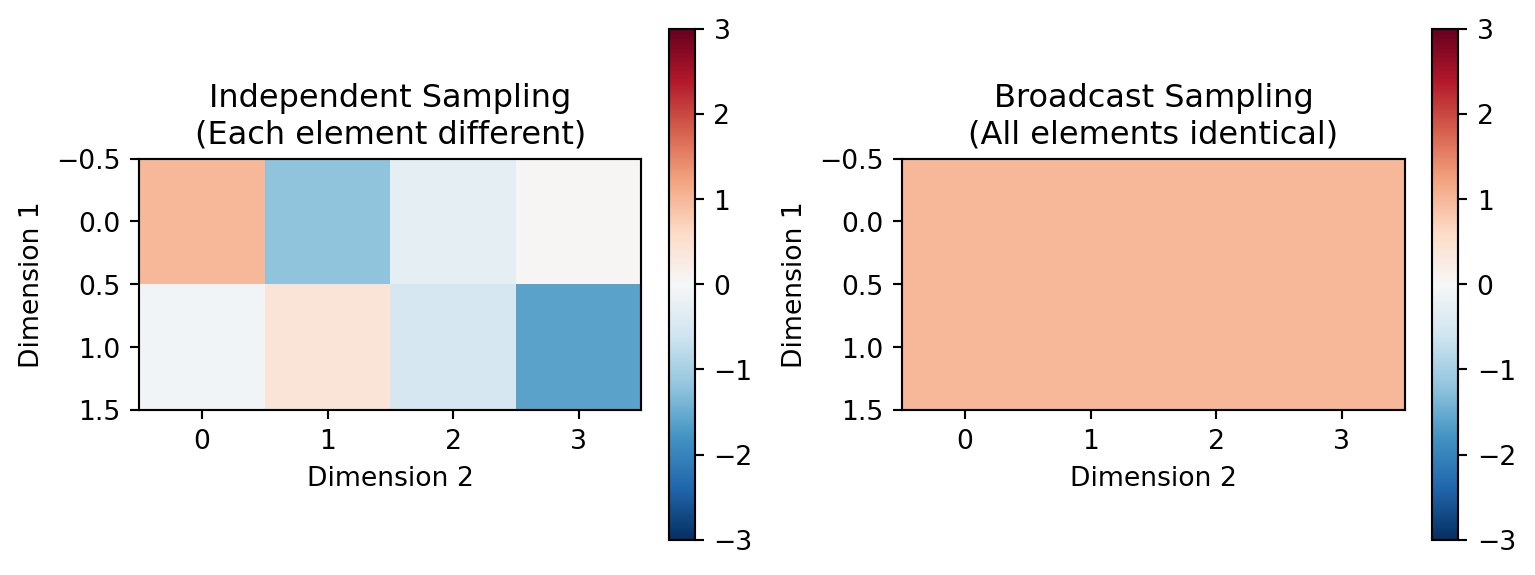
### Independent vs Broadcast Sampling
NumPyroAxis supports two sampling modes for different modeling scenarios:
```{python}
key = jax.random.key(456)
# Independent mode: each element sampled independently
independent_axis = NumPyroAxis(
dist.Normal(0.0, 1.0),
n=3,
sample_shape=(2, 4),
broadcast_mode=False
)
independent_samples = independent_axis.generate_values(key)
# Broadcast mode: one sample per axis point, broadcast to shape
broadcast_axis = NumPyroAxis(
dist.Normal(0.0, 1.0),
n=3,
sample_shape=(2, 4),
broadcast_mode=True
)
broadcast_samples = broadcast_axis.generate_values(key)
print("Independent sampling:")
print(f"Shape: {independent_samples.shape}")
print("Sample 0 (each element different):")
print(independent_samples[0])
print()
print("Broadcast sampling:")
print(f"Shape: {broadcast_samples.shape}")
print("Sample 0 (all elements identical):")
print(broadcast_samples[0])
print(f"All elements identical: {jnp.allclose(broadcast_samples[0], broadcast_samples[0].flatten()[0])}")
```
```{python}
#| code-fold: true
#| code-summary: "Show visualization code"
# Visualize the difference
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8.1, 4))
# Independent sampling heatmap
im1 = ax1.imshow(independent_samples[0], cmap='RdBu_r', vmin=-3, vmax=3)
ax1.set_title('Independent Sampling\n(Each element different)')
ax1.set_xlabel('Dimension 2')
ax1.set_ylabel('Dimension 1')
plt.colorbar(im1, ax=ax1, fraction=0.046)
# Broadcast sampling heatmap
im2 = ax2.imshow(broadcast_samples[0], cmap='RdBu_r', vmin=-3, vmax=3)
ax2.set_title('Broadcast Sampling\n(All elements identical)')
ax2.set_xlabel('Dimension 2')
ax2.set_ylabel('Dimension 1')
plt.colorbar(im2, ax=ax2, fraction=0.046)
plt.tight_layout()
plt.show()
```
# Composing with Space
## Basic Space Creation
The `Space` class is where the magic happens - it takes a state tree containing axes and fixed values, then creates all possible parameter combinations according to your specified strategy.
```{python}
# Create a realistic brain simulation parameter space
simulation_state = {
'coupling': {
'strength': GridAxis(0.1, 0.8, 5), # Coupling strength
'delay': UniformAxis(5.0, 25.0, 3), # Transmission delays (ms)
},
'model': {
'noise_amplitude': DataAxis([0.01, 0.02, 0.05]), # Noise levels from pilot study
'time_constant': 10.0, # Fixed parameter
},
'simulation': {
'dt': 0.1, # Fixed time step
'duration': 1000, # Fixed duration
}
}
# Create the space
space = Space(simulation_state, mode='product', key=jax.random.key(789))
print(f"Parameter space contains {len(space)} combinations")
print(f"Combination modes: 5 × 3 × 3 = {5*3*3} (Grid × Uniform × Data)")
# Look at a few parameter combinations
print("\nFirst 3 parameter combinations:")
print("=" * 50)
for i, params in enumerate(space):
if i >= 3: break
print(f"\nCombination {i}:")
print(f" Coupling strength: {params['coupling']['strength']:.3f}")
print(f" Coupling delay: {params['coupling']['delay']:.2f} ms")
print(f" Noise amplitude: {params['model']['noise_amplitude']:.3f}")
print(f" Time constant: {params['model']['time_constant']} (fixed)")
print(f" Simulation dt: {params['simulation']['dt']} (fixed)")
```
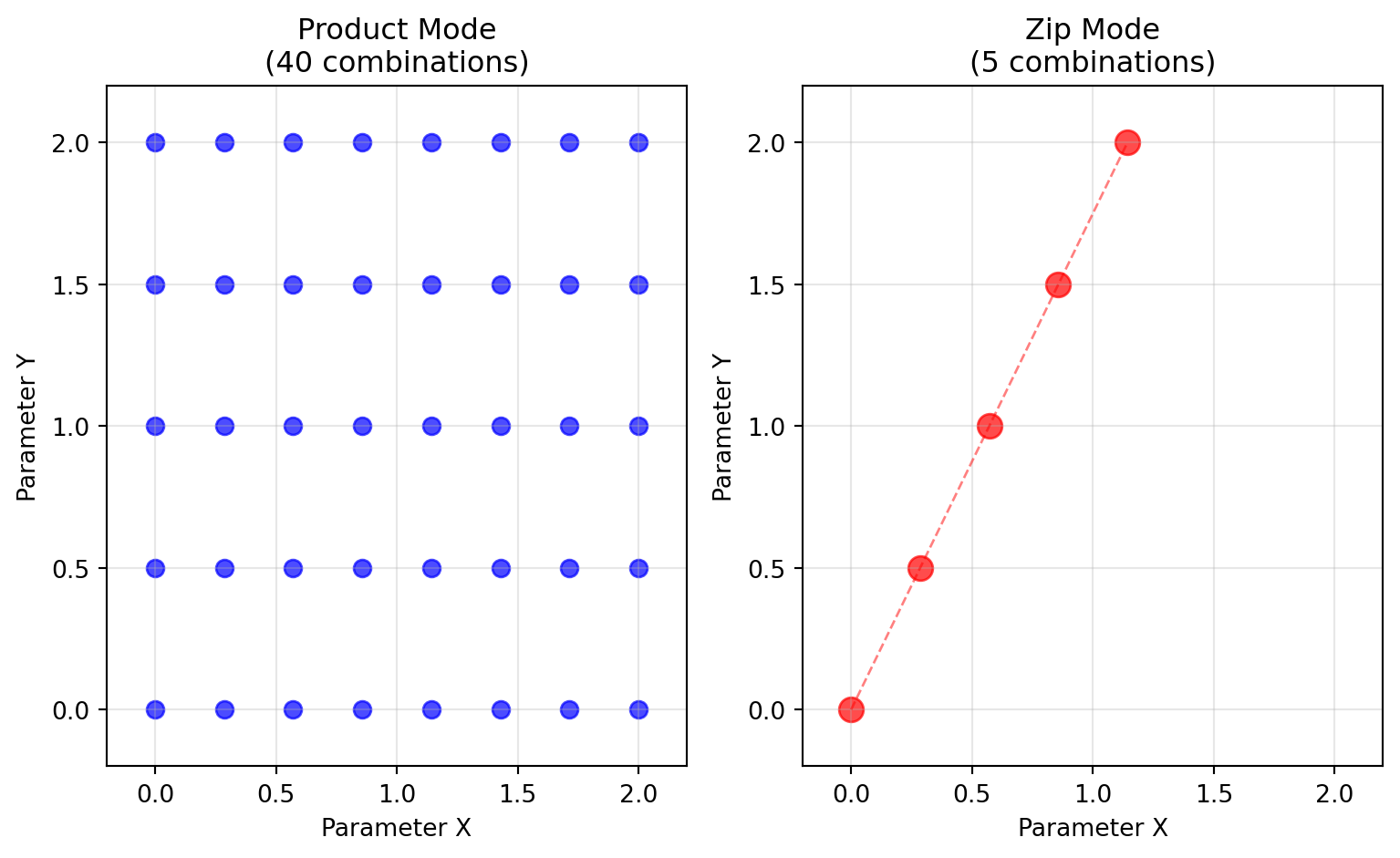
## Combination Modes: Product vs Zip
The two combination modes serve different exploration strategies:
### Product Mode (Cartesian Product)
Perfect for **systematic exploration** - tests every combination of parameter values.
```{python}
# Product mode: systematic exploration
product_state = {
'param_a': GridAxis(0.0, 1.0, 3),
'param_b': GridAxis(0.0, 1.0, 2),
}
product_space = Space(product_state, mode='product')
print(f"Product mode: {len(product_space)} combinations")
print("\nAll combinations (product mode):")
for i, params in enumerate(product_space):
print(f" {i}: a={params['param_a']:.1f}, b={params['param_b']:.1f}")
```
### Zip Mode (Parallel Sampling)
Perfect for **matched sampling** - pairs corresponding elements from each axis.
```{python}
# Zip mode: matched sampling
zip_space = Space(product_state, mode='zip')
print(f"Zip mode: {len(zip_space)} combinations (uses minimum axis size)")
print("\nMatched combinations (zip mode):")
for i, params in enumerate(zip_space):
print(f" {i}: a={params['param_a']:.1f}, b={params['param_b']:.1f}")
```
```{python}
#| code-fold: true
#| code-summary: "Show visualization code"
# Create a more interesting comparison
comparison_state = {
'x': GridAxis(0.0, 2.0, 8),
'y': GridAxis(0.0, 2.0, 5),
}
product_comp = Space(comparison_state, mode='product')
zip_comp = Space(comparison_state, mode='zip')
# Extract coordinates for plotting
product_x = [p['x'] for p in product_comp]
product_y = [p['y'] for p in product_comp]
zip_x = [p['x'] for p in zip_comp]
zip_y = [p['y'] for p in zip_comp]
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8.1, 5))
# Product mode visualization
ax1.scatter(product_x, product_y, color='blue', s=50, alpha=0.7)
ax1.set_xlabel('Parameter X')
ax1.set_ylabel('Parameter Y')
ax1.set_title(f'Product Mode\n({len(product_comp)} combinations)')
ax1.grid(True, alpha=0.3)
ax1.set_xlim(-0.2, 2.2)
ax1.set_ylim(-0.2, 2.2)
# Zip mode visualization
ax2.scatter(zip_x, zip_y, color='red', s=100, alpha=0.7)
ax2.plot(zip_x, zip_y, 'r--', alpha=0.5, linewidth=1)
ax2.set_xlabel('Parameter X')
ax2.set_ylabel('Parameter Y')
ax2.set_title(f'Zip Mode\n({len(zip_comp)} combinations)')
ax2.grid(True, alpha=0.3)
ax2.set_xlim(-0.2, 2.2)
ax2.set_ylim(-0.2, 2.2)
plt.tight_layout()
plt.show()
```
## Iteration & Access Patterns
Space provides flexible ways to access parameter combinations:
```{python}
# Create a space for demonstration
demo_state = {
'coupling': GridAxis(0.0, 1.0, 6),
'noise': UniformAxis(0.01, 0.1, 6),
'threshold': 0.5 # Fixed value
}
demo_space = Space(demo_state, mode='zip', key=jax.random.key(42))
print(f"Demo space has {len(demo_space)} combinations")
```
### Sequential Iteration
```{python}
# Standard iteration - perfect for simulations
print("Sequential iteration (first 3):")
for i, params in enumerate(demo_space):
if i >= 3: break
print(f" Run {i}: coupling={params['coupling']:.2f}, "
f"noise={params['noise']:.4f}")
```
### Random Access
```{python}
# Direct indexing - great for debugging specific combinations
print("Random access examples:")
print(f" Combination 0: coupling = {demo_space[0]['coupling']:.3f}")
print(f" Combination 2: coupling = {demo_space[2]['coupling']:.3f}")
print(f" Last combination: coupling = {demo_space[-1]['coupling']:.3f}")
# Negative indexing works too
print(f" Second to last: coupling = {demo_space[-2]['coupling']:.3f}")
```
### Slicing for Subset Analysis
```{python}
# Slicing creates new spaces - perfect for subset analysis
subset = demo_space[1:4]
print(f"Subset contains {len(subset)} combinations")
print("Subset combinations:")
for i, params in enumerate(subset):
print(f" Original index {i+1}: coupling={params['coupling']:.3f}")
# Slicing with steps
every_other = demo_space[::2]
print(f"\nEvery other combination ({len(every_other)} total):")
for i, params in enumerate(every_other):
print(f" Index {i}: coupling={params['coupling']:.3f}")
```
# Execution: Running Functions Over Spaces
Now that we understand how to create and manipulate parameter spaces, let's see how to actually execute functions over them. TVB-Optim provides two execution strategies through `SequentialExecution` and `ParallelExecution` classes.
## Sequential Execution
Sequential execution processes parameter combinations one at a time, making it ideal for debugging, memory-constrained environments, or when you need full control over execution order.
```{python}
from tvboptim.execution import SequentialExecution
# Define a simple brain simulation model
def brain_simulation(state, noise_factor=1.0):
"""
Simple brain simulation that combines coupling and noise.
Returns both simulation results and metadata.
"""
coupling = state['coupling']
noise = state['noise'] * noise_factor
# Simulate some dynamics (simplified for demonstration)
activity = coupling * jnp.sin(jnp.linspace(0, 4*jnp.pi, 100)) + noise * jax.random.normal(jax.random.key(42), shape=(100,))
# Calculate some metrics
mean_activity = jnp.mean(activity)
peak_activity = jnp.max(activity)
return {
'activity': activity,
'metrics': {
'mean': mean_activity,
'peak': peak_activity,
'coupling_used': coupling,
'noise_used': noise
}
}
# Create a parameter space for our simulation
simulation_state = {
'coupling': GridAxis(0.2, 1.5, 4),
'noise': UniformAxis(0.01, 0.1, 4),
'fixed_param': 42.0
}
space = Space(simulation_state, mode='zip', key=jax.random.key(123))
print(f"Parameter space: {len(space)} combinations")
# Set up sequential execution
sequential_executor = SequentialExecution(
model=brain_simulation,
statespace=space,
noise_factor=1.5 # Additional parameter passed to model
)
print("\nExecuting simulations sequentially...")
```
```{python}
# Run the sequential execution (with progress bar)
sequential_results = sequential_executor.run()
print(f"Execution complete! Got {len(sequential_results)} results")
# Access results
first_result = sequential_results[0]
print(f"\nFirst result structure:")
print(f" Activity shape: {first_result['activity'].shape}")
print(f" Mean activity: {first_result['metrics']['mean']:.3f}")
print(f" Peak activity: {first_result['metrics']['peak']:.3f}")
print(f" Coupling used: {first_result['metrics']['coupling_used']:.3f}")
# Analyze all results
print(f"\nAll simulation metrics:")
for i, result in enumerate(sequential_results):
metrics = result['metrics']
print(f" Run {i}: coupling={metrics['coupling_used']:.2f}, "
f"noise={metrics['noise_used']:.4f}, mean={metrics['mean']:.3f}")
```
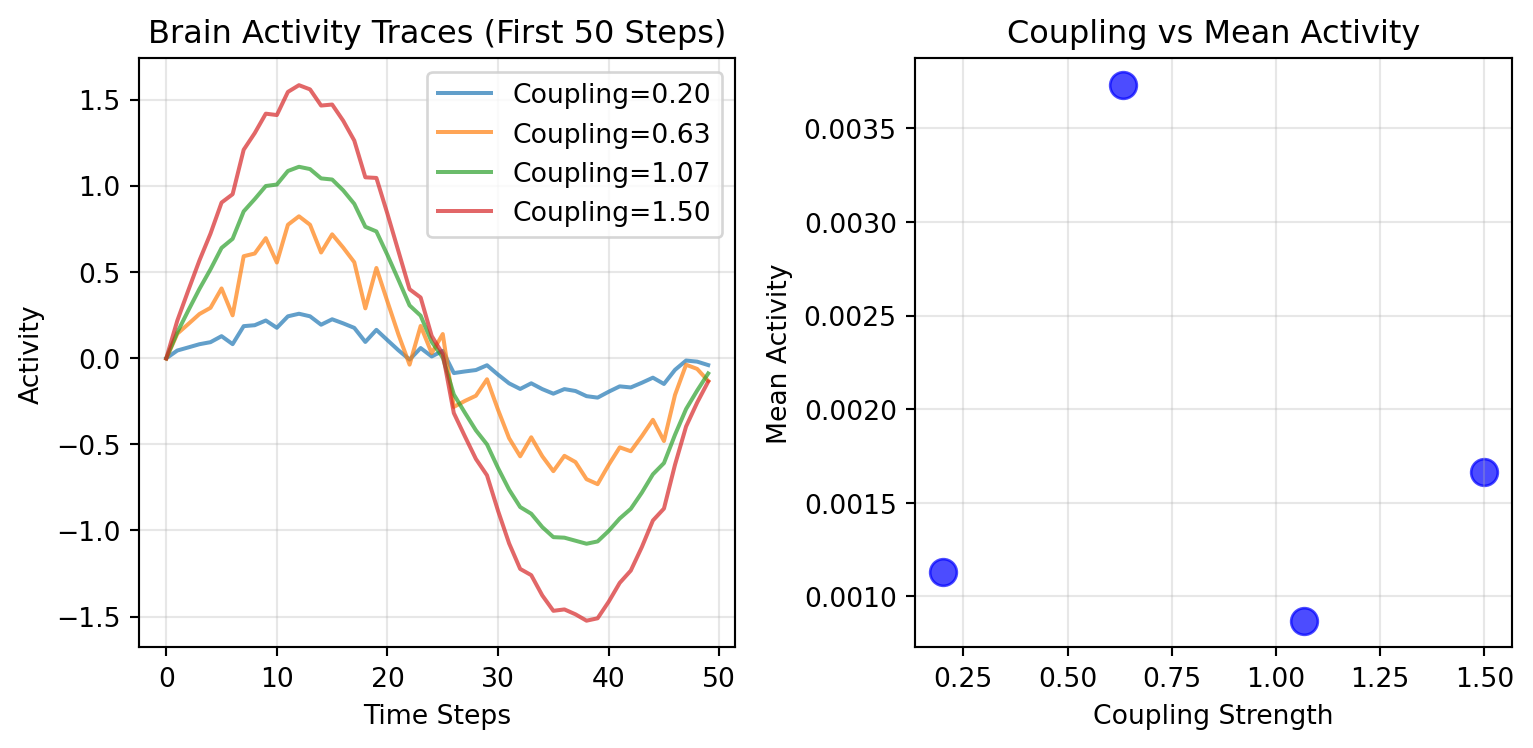
```{python}
#| code-fold: true
#| code-summary: "Show visualization code"
# Visualize sequential execution results
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8.1, 4))
# Plot activity traces
for i, result in enumerate(sequential_results):
activity = result['activity']
coupling = result['metrics']['coupling_used']
ax1.plot(activity[:50], alpha=0.7, label=f'Coupling={coupling:.2f}')
ax1.set_xlabel('Time Steps')
ax1.set_ylabel('Activity')
ax1.set_title('Brain Activity Traces (First 50 Steps)')
ax1.legend()
ax1.grid(True, alpha=0.3)
# Plot coupling vs mean activity relationship
couplings = [r['metrics']['coupling_used'] for r in sequential_results]
means = [r['metrics']['mean'] for r in sequential_results]
ax2.scatter(couplings, means, s=100, alpha=0.7, color='blue')
ax2.set_xlabel('Coupling Strength')
ax2.set_ylabel('Mean Activity')
ax2.set_title('Coupling vs Mean Activity')
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
## Parallel Execution
Parallel execution leverages JAX's `pmap` and `vmap` transformations for efficient vectorized computation across multiple devices. This is essential for large-scale parameter explorations.
```{python}
from tvboptim.execution import ParallelExecution
# Create a larger parameter space for parallel execution
parallel_state = {
'coupling': GridAxis(0.1, 2.0, 8),
'noise': UniformAxis(0.005, 0.05, 8),
'threshold': 0.5 # Fixed parameter
}
parallel_space = Space(parallel_state, mode='product', key=jax.random.key(456))
print(f"Larger parameter space: {len(parallel_space)} combinations")
# Define a JAX-optimized model for parallel execution
def fast_brain_model(state):
"""
JAX-optimized brain model for parallel execution.
Simpler than sequential version for faster computation.
"""
coupling = state['coupling']
noise = state['noise']
# Simplified dynamics that's faster to compute
base_activity = coupling * jnp.sin(jnp.arange(20) * 0.5)
noisy_activity = base_activity + noise * jax.random.normal(jax.random.key(123), shape=(20,))
return {
'mean_activity': jnp.mean(noisy_activity),
'max_activity': jnp.max(noisy_activity),
'params': state
}
# Set up parallel execution
n_devices = jax.device_count()
print(f"Available devices: {n_devices}")
parallel_executor = ParallelExecution(
model=fast_brain_model,
space=parallel_space,
n_vmap=8, # Vectorize over 8 parameter combinations
n_pmap=1 # Use 1 device (can use more if available)
)
print("\nExecuting simulations in parallel...")
```
```{python}
# Run parallel execution
parallel_results = parallel_executor.run()
print(f"Parallel execution complete! Got {len(parallel_results)} results")
# Access results - same interface as sequential
first_parallel = parallel_results[0]
print(f"\nFirst parallel result:")
print(f" Mean activity: {first_parallel['mean_activity']:.3f}")
print(f" Max activity: {first_parallel['max_activity']:.3f}")
print(f" Coupling: {first_parallel['params']['coupling']:.3f}")
# Get subset of results
subset_results = parallel_results[5:15]
print(f"\nSubset contains {len(subset_results)} results")
# Analyze parameter-activity relationships
couplings = [r['params']['coupling'] for r in parallel_results]
means = [r['mean_activity'] for r in parallel_results]
max_vals = [r['max_activity'] for r in parallel_results]
print(f"\nParameter exploration summary:")
print(f" Coupling range: [{min(couplings):.2f}, {max(couplings):.2f}]")
print(f" Mean activity range: [{min(means):.3f}, {max(means):.3f}]")
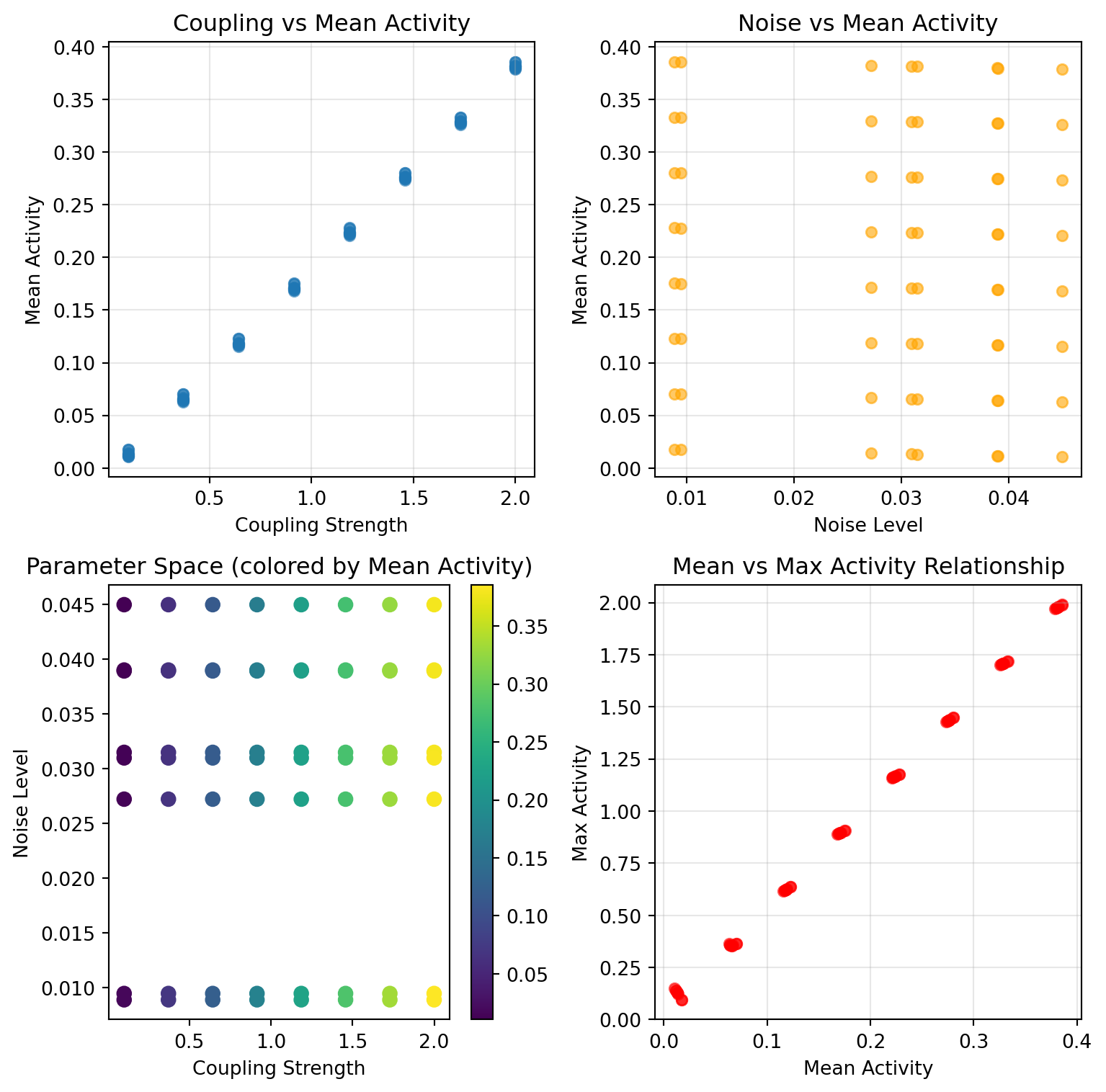
print(f" Max activity range: [{min(max_vals):.3f}, {max(max_vals):.3f}]")
```
```{python}
#| code-fold: true
#| code-summary: "Show visualization code"
# Visualize parallel execution results
fig, axes = plt.subplots(2, 2, figsize=(8.1, 8))
# 1. Coupling vs Mean Activity
ax = axes[0, 0]
ax.scatter(couplings, means, alpha=0.6, s=30)
ax.set_xlabel('Coupling Strength')
ax.set_ylabel('Mean Activity')
ax.set_title('Coupling vs Mean Activity')
ax.grid(True, alpha=0.3)
# 2. Noise vs Mean Activity
noises = [r['params']['noise'] for r in parallel_results]
ax = axes[0, 1]
ax.scatter(noises, means, alpha=0.6, s=30, color='orange')
ax.set_xlabel('Noise Level')
ax.set_ylabel('Mean Activity')
ax.set_title('Noise vs Mean Activity')
ax.grid(True, alpha=0.3)
# 3. 2D parameter space visualization
ax = axes[1, 0]
scatter = ax.scatter(couplings, noises, c=means, cmap='viridis', s=50)
ax.set_xlabel('Coupling Strength')
ax.set_ylabel('Noise Level')
ax.set_title('Parameter Space (colored by Mean Activity)')
plt.colorbar(scatter, ax=ax)
# 4. Mean vs Max Activity
ax = axes[1, 1]
ax.scatter(means, max_vals, alpha=0.6, s=30, color='red')
ax.set_xlabel('Mean Activity')
ax.set_ylabel('Max Activity')
ax.set_title('Mean vs Max Activity Relationship')
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
## Performance Comparison & Best Practices
```{python}
import time
# Compare execution times for different approaches
small_state = {
'param1': GridAxis(0.0, 1.0, 5),
'param2': UniformAxis(0.0, 1.0, 5)
}
small_space = Space(small_state, mode='product', key=jax.random.key(789))
def simple_model(state):
return {'result': state['param1'] * state['param2']}
print("Performance comparison on 25 parameter combinations:")
print("=" * 55)
# Sequential timing
seq_exec = SequentialExecution(simple_model, small_space)
start = time.time()
seq_results = seq_exec.run()
seq_time = time.time() - start
print(f"Sequential execution: {seq_time:.4f} seconds")
# Parallel timing
par_exec = ParallelExecution(simple_model, small_space, n_vmap=5, n_pmap=1)
start = time.time()
par_results = par_exec.run()
par_time = time.time() - start
print(f"Parallel execution: {par_time:.4f} seconds")
if seq_time > par_time:
speedup = seq_time / par_time
print(f"Parallel speedup: {speedup:.1f}x faster")
else:
print("Sequential was faster (overhead dominates for small problems)")
print(f"\nBoth produced {len(seq_results)} results")
```
### When to Use Each Approach
**Sequential Execution:**
- **Debugging**: Easy to trace through individual parameter combinations
- **Memory constraints**: Processes one combination at a time
- **Complex models**: When models don't easily vectorize
- **Small parameter spaces**: Overhead of parallelization not worth it
**Parallel Execution:**
- **Large parameter spaces**: Massive speedups for hundreds/thousands of combinations
- **JAX-compatible models**: Models that can be easily vectorized
- **Production runs**: When you need results fast
- **Multi-device setups**: Can leverage multiple GPUs/TPUs
### Integration with Spaces
Both execution types work seamlessly with all space features:
```{python}
# Works with any axis type
complex_state = {
'coupling': NumPyroAxis(dist.Beta(2.0, 5.0), n=3), # Probabilistic
'delay': DataAxis([5.0, 10.0, 15.0]), # Specific values
'noise': GridAxis(0.01, 0.1, 3), # Systematic
'region_params': 68.0 # Fixed value
}
complex_space = Space(complex_state, mode='product', key=jax.random.key(999))
print(f"Complex space: {len(complex_space)} combinations")
# Both executors handle this seamlessly
print("✓ Sequential execution: handles any space complexity")
print("✓ Parallel execution: vectorizes over any parameter combination")
print("✓ Results: same access patterns regardless of execution type")
```
This execution system provides the final piece of the TVB-Optim parameter exploration pipeline - taking your carefully designed parameter spaces and efficiently computing results across all combinations, whether you need the control of sequential execution or the speed of parallel execution.