Parameters and Optimization in TVB-Optim

Why Parameters?

Parameters serve two purposes:

  1. Define which values get differentiated and subsequently optimized.
  2. Enforce constraints during optimization by applying transformations, eg a positive constraint on a parameter.

General Properties of Parameters

Parameters define the __jax_array__ method, which allows us to use them in the same way as jax arrays.

import jax
import jax.numpy as jnp

from tvboptim.types import Parameter

p = Parameter(jnp.array([1.0, 2.0, 3.0]))

print("Shape:", p.shape)
print("Numeric op:", p + 1)
print("Jax op:", jnp.sin(p))
Shape: (3,)
Numeric op: [2. 3. 4.]
Jax op: [0.84147096 0.9092974  0.14112   ]

It is good practice to only use parameters for optimization and collect them afterwards for postprocessing as the __jax_array__ protocol is still experimental (More info) and might lead to unexpected results.

from tvboptim.types import collect_parameters

collect_parameters(p) # collect all arrays from the Parameters in a PyTree
Array([1., 2., 3.], dtype=float32)

Marking Parameters for Optimization

After using prepare on an experiment (TVB-O) or network (tvboptim.experimental.network_dynamics), we have a state object which is a PyTree with jax arrays at its leaves. The state helps structuring the many values and inputs needed for the simulation in a simple object for convenience. But in most cases we only want to subject a fraction of the state to optimization. We can mark the values in the state for optimization by wrapping them in the Parameter type:

from tvboptim.experimental.network_dynamics import Bunch # A dictionary with attribute access

from tvboptim.types import Parameter, show_parameters

# A simple example state
simple_state = Bunch(
    global_coupling = 0.1,
    time_constant = 1.0,
)

# Mark global coupling for optimization
simple_state.global_coupling = Parameter(simple_state.global_coupling)

show_parameters(simple_state)
Parameters
├── global_coupling
│   └── value: 0.10000000149011612

Inside e.g. OptaxOptimizer we can use the knowledge of what to consider a parameter to partition the state into two sub PyTrees, one that gets differentiated and one that stays static:

from tvboptim.types import partition_state, combine_state

diff_state, static_state = partition_state(simple_state)

print("Diff state:")
print(diff_state)
print("Static state:")
print(static_state)
Diff state:
Bunch(global_coupling=Parameter(0.10000000149011612), time_constant=None)
Static state:
Bunch(global_coupling=None, time_constant=1.0)

Sub PyTrees can be combined back to a single PyTree using combine_state. This is something that the OptaxOptimizer does automatically.

# Schematics of the `OptaxOptimizer`
def loss_wrapper(diff_state, static_state):
    state = combine_state(diff_state, static_state) # Recombine parameters with static values
    return loss(state)

jax.grad(loss_wrapper)(diff_state, static_state) # grad by default acts only on the first argument

Enforcing Constraints

Some values in a model can be constrained through their physiological meaning. For example, we want the global coupling to be positive. The optimizer itself does not know about these constraints, so we have to apply them explicitly.

from tvboptim.types import BoundedParameter

p1 = Parameter(-0.0001)
p2 = BoundedParameter(0.5, low=0.0, high=1.0)
p3 = BoundedParameter(-0.0001, low=0.0, high=1.0)

# Simple loss that would increase p to infinity in minimization
def loss(p):
    return -p

print("Gradient without constraint:", jax.grad(loss)(p1))
print("Gradient with fulfilled constraint:", jax.grad(loss)(p2))
print("Gradient with violated constraint:", jax.grad(loss)(p3))
Gradient without constraint: Parameter(-1.0)
Gradient with fulfilled constraint: BoundedParameter(-1.0, low=0.0, high=1.0)
Gradient with violated constraint: BoundedParameter(-0.0, low=0.0, high=1.0)

We provide several predefined parameter types:

  • Parameter
  • BoundedParameter
  • NormalizedParameter
  • TransformedParameter
  • SigmoidBoundedParameter
  • MaskedParameter

Custom constraints can be implemented as well, for that either Parameter can be subclassed directly or we use TransformedParameter and define our constraint as forward and reverse transforms. As an example lets look at how we would build a sigmoid bounded parameter. This has the advantage over BoundedParameter that we always get a gradient, while the BoundedParameter returns 0 when the constraint is violated and it then stays at the lower or upper bound indefinitely.

from tvboptim.types import TransformedParameter, SigmoidBoundedParameter

def sigmoid_bounded_param(value, low=0.0, high=1.0):
    def forward(x):
        return low + (high - low) * jax.nn.sigmoid(x)
    def inverse(x):
        normalized = (x - low) / (high - low)
        return jnp.log(normalized / (1 - normalized))
    return TransformedParameter(value, forward, inverse)

# Check if the constraint is fulfilled
p_custom = sigmoid_bounded_param(0.5, low=0.0, high=1.0)

print("Custom TransformedParameter:", p_custom)
print("Gradient with smooth constraint:", jax.grad(loss)(p_custom))
Custom TransformedParameter: TransformedParameter(original=0.5, transformed=0.0)
Gradient with smooth constraint: TransformedParameter(original=0.43782350420951843, transformed=-0.25)

To check if the constraint is fulfilled we run an Optimization on the simple loss function, the parameter should stay below 1:

from tvboptim.optim import OptaxOptimizer
import optax

opt = OptaxOptimizer(loss, optax.adam(0.01))
p_opt, _ = opt.run(p_custom, max_steps=1000)
print("Optimized parameter:", p_opt)
print("Smaller than 1:", p_opt < 1.0)
Optimized parameter: TransformedParameter(original=0.9860481023788452, transformed=4.258087158203125)
Smaller than 1: True

A Simple Example

As a simple example on how to use parameters we try to find the fixed point of the reduced Wong-Wang model. This example demonstrates the key concepts of parameter optimization in TVB-Optim by finding parameter values where the neural activity reaches equilibrium.

Setting up the Model

First, we load the reduced Wong-Wang model and examine its structure:

from tvboptim.experimental.network_dynamics.dynamics import ReducedWongWang

m = ReducedWongWang()

dfun = m.dynamics

m.DEFAULT_PARAMS
Bunch(a=0.27, b=0.108, d=154.0, gamma=0.641, tau_s=100.0, w=0.6, J_N=0.2609, I_o=0.33)

The model includes parameters like gamma (kinetic parameter) and tau_s (time constant) that control the dynamics.

Defining the Optimization Problem

For a specific initial condition and coupling, we have a fixed point if the derivative is zero. We define our loss function to minimize the absolute sum of derivatives:

p_init = m.DEFAULT_PARAMS

def loss_fixed_point(p, S_0 = [0.8], coupling = Bunch(instant = [0.0], delayed = [0.0])):
    return jnp.abs(jnp.sum(dfun(0.0, S_0, p, coupling, coupling)[0]))

print(f"Initial loss: {loss_fixed_point(p_init):.6f}")
Initial loss: 0.005874

Without parameter constraints, JAX would differentiate all parameters in the model:

gradients = jax.grad(loss_fixed_point)(p_init)
print("Gradients for all parameters:", gradients)
Gradients for all parameters: Bunch(I_o=Array(-0.02859925, dtype=float32, weak_type=True), J_N=Array(-0.01372764, dtype=float32, weak_type=True), a=Array(-0.04821961, dtype=float32, weak_type=True), b=Array(0.10592316, dtype=float32, weak_type=True), d=Array(3.5458395e-06, dtype=float32, weak_type=True), gamma=Array(-0.00331615, dtype=float32, weak_type=True), tau_s=Array(-8.e-05, dtype=float32, weak_type=True), w=Array(-0.00596924, dtype=float32, weak_type=True))

Running the Optimization

Now we’ll set up and run the optimization using both regular and normalized parameters to compare their performance.

Setting up the Optimizer

We configure the optimizer with callbacks to track progress and automatically stop when convergence is achieved:

from tvboptim.optim import OptaxOptimizer, DefaultPrintCallback, StopLossCallback, SavingLossCallback, SavingParametersCallback, MultiCallback
import optax

# Configure callbacks for monitoring optimization progress
cbs = MultiCallback([
    DefaultPrintCallback(every=10),      # Print progress every 10 steps
    SavingLossCallback(),                # Save loss history
    SavingParametersCallback(),          # Save parameter history
    StopLossCallback(stop_loss=1e-6),    # Stop when loss is sufficiently small
])

opt = OptaxOptimizer(loss_fixed_point, optax.adam(0.01), callback=cbs)

Optimization with Regular Parameters

First, let’s optimize using regular Parameter objects, focusing only on gamma and tau_s:

# Mark specific parameters for optimization
p_init.gamma = Parameter(p_init.gamma)
p_init.tau_s = Parameter(p_init.tau_s)

print("Starting optimization with regular Parameters...")
p_opt, fitting_data = opt.run(p_init, max_steps=1000)
print(f"Final loss: {fitting_data['loss'].save.values[-1]:.8f}")
Starting optimization with regular Parameters...
Step 0: 0.005874
Step 10: 0.005535
Step 20: 0.005195
Step 30: 0.004856
Step 40: 0.004516
Step 50: 0.004177
Step 60: 0.003837
Step 70: 0.003498
Step 80: 0.003158
Step 90: 0.002819
Step 100: 0.002479
Step 110: 0.002140
Step 120: 0.001801
Step 130: 0.001461
Step 140: 0.001122
Step 150: 0.000783
Step 160: 0.000443
Step 170: 0.000104
Step 180: 0.000114
Step 190: 0.000014
Step 200: 0.000002
Step 210: 0.000015
Stopped at step 218 with loss 0.000001
Stopping due to callback
Final loss: 0.00000059

Optimization with Normalized Parameters

Now let’s compare with NormalizedParameter, which can lead to better convergence by normalizing parameter scales (gamma = 0.681 -> 1.0, tau_s = 100 -> 1.0):

from tvboptim.types import NormalizedParameter
# Reset and use normalized parameters
p_init.gamma = NormalizedParameter(p_init.gamma)
p_init.tau_s = NormalizedParameter(p_init.tau_s)

print("Starting optimization with NormalizedParameters...")
p_opt_norm, fitting_data_norm = opt.run(p_init, max_steps=1000)
print(f"Final loss: {fitting_data_norm['loss'].save.values[-1]:.8f}")
Starting optimization with NormalizedParameters...
Step 0: 0.005874
Step 10: 0.004939
Step 20: 0.004142
Step 30: 0.003457
Step 40: 0.002860
Step 50: 0.002327
Step 60: 0.001845
Step 70: 0.001401
Step 80: 0.000987
Step 90: 0.000596
Step 100: 0.000224
Step 110: 0.000093
Step 120: 0.000048
Step 130: 0.000034
Step 140: 0.000003
Step 150: 0.000008
Step 160: 0.000000
Stopped at step 160 with loss 0.000000
Stopping due to callback
Final loss: 0.00000025

Comparing Optimization Performance

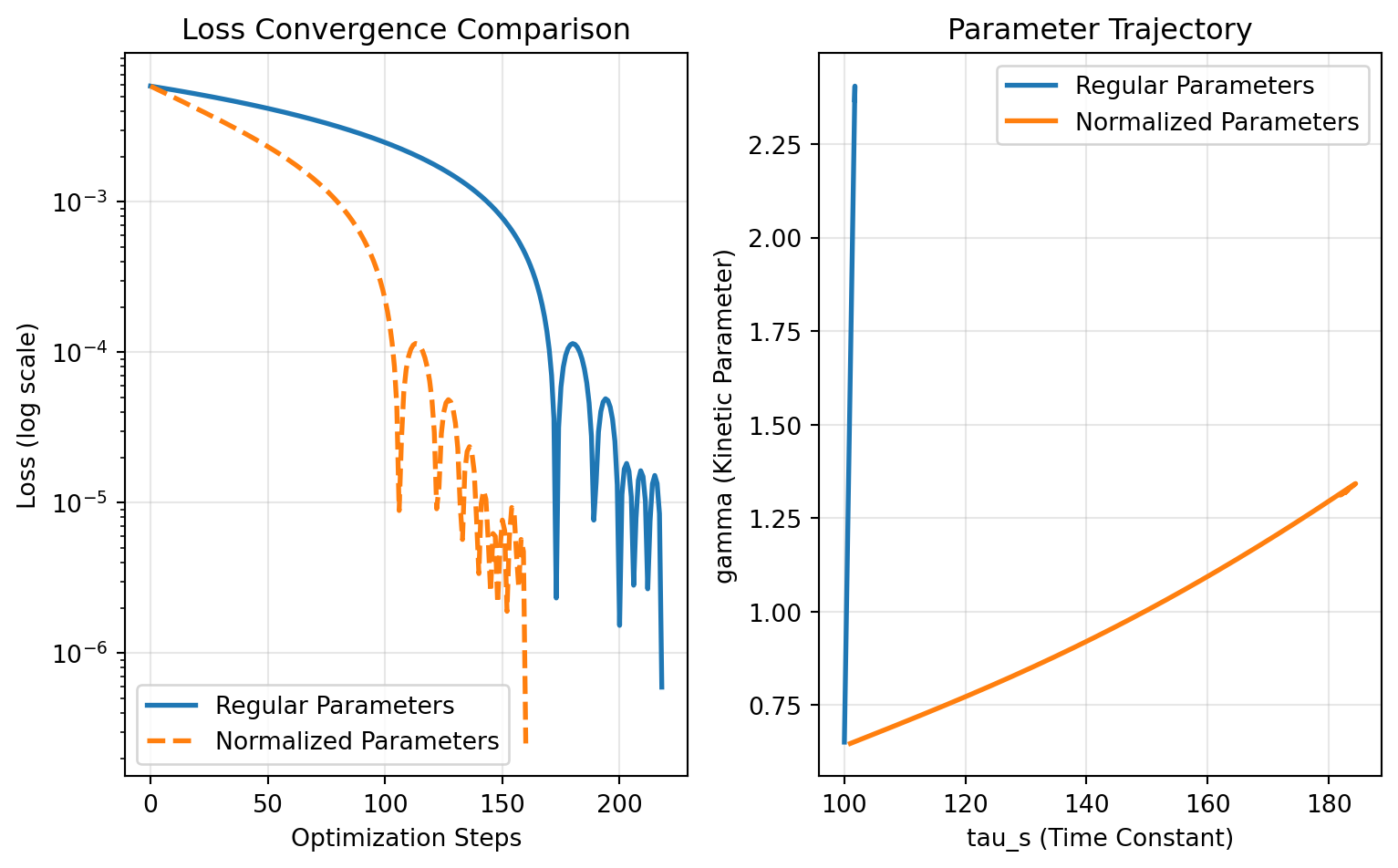
The normalized parameters converge faster than regular parameters. With regular Parameter objects alone, most of the optimization change was applied to gamma while tau_s barely changed due to scaling differences and a learning rate of 0.01.

Visualization of Convergence

Let’s create plots to visualize the optimization convergence and parameter trajectories:

Show visualization code 
import matplotlib.pyplot as plt

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8.1, 5.0625))

# Loss convergence comparison
ax1.semilogy(fitting_data["loss"].save, label='Regular Parameters', linewidth=2)
ax1.semilogy(fitting_data_norm["loss"].save, label='Normalized Parameters', linewidth=2, linestyle='--')
ax1.set_xlabel('Optimization Steps')
ax1.set_ylabel('Loss (log scale)')
ax1.set_title('Loss Convergence Comparison')
ax1.legend()
ax1.grid(True, alpha=0.3)

# Parameter trajectory in 2D space
gamma_traj = collect_parameters([p.gamma for p in fitting_data["parameters"].save])
tau_s_traj = collect_parameters([p.tau_s for p in fitting_data["parameters"].save])
gamma_traj_norm = collect_parameters([p.gamma for p in fitting_data_norm["parameters"].save])
tau_s_traj_norm = collect_parameters([p.tau_s for p in fitting_data_norm["parameters"].save])

ax2.plot(tau_s_traj, gamma_traj, label='Regular Parameters', linewidth=2)
ax2.plot(tau_s_traj_norm, gamma_traj_norm, label='Normalized Parameters', linewidth=2)
ax2.set_xlabel('tau_s (Time Constant)')
ax2.set_ylabel('gamma (Kinetic Parameter)')
ax2.set_title('Parameter Trajectory')
ax2.legend()
ax2.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

Validating the Fixed Point Solution

Finally, let’s run simulations with the optimized parameters to verify that we’ve achieved the desired fixed point at 0.8:

# Run simulation with default parameters
m = ReducedWongWang()
ts_default = m.simulate(t1 = 1000, dt = 1.0)

# Run simulation with optimized parameters (regular Parameter)
p_opt = collect_parameters(p_opt)
m = ReducedWongWang(gamma = p_opt.gamma, tau_s = p_opt.tau_s)
ts_opt = m.simulate(t1 = 1000, dt = 1.0)

# Run simulation with optimized normalized parameters
p_opt_norm = collect_parameters(p_opt_norm)
m = ReducedWongWang(gamma = p_opt_norm.gamma, tau_s = p_opt_norm.tau_s)
ts_opt_norm = m.simulate(t1 = 1000, dt = 1.0)

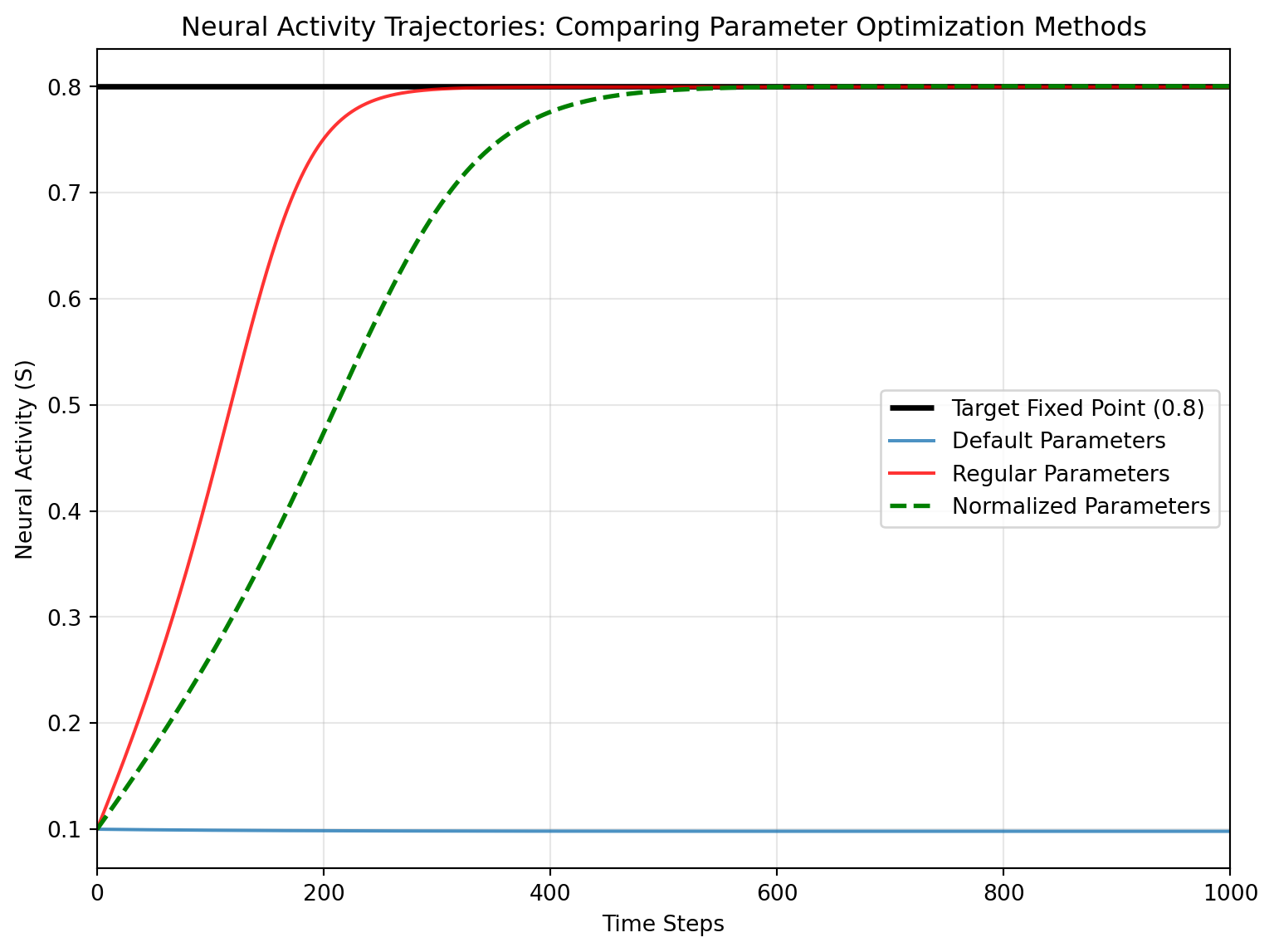
Now let’s visualize how well each optimization approach achieved the target fixed point:

Show visualization code 
fig, ax = plt.subplots(figsize=(8.1, 6.075))

# Plot target line
ax.hlines(0.8, 0, 1000, color="black", linewidth=2.5, label="Target Fixed Point (0.8)")

# Plot time series
ax.plot(ts_default[1][:, 0, :], label="Default Parameters", alpha=0.8)
ax.plot(ts_opt[1][:, 0, :], color='red', label="Regular Parameters", alpha=0.8)
ax.plot(ts_opt_norm[1][:, 0, :], color='green', linestyle='--',
        label="Normalized Parameters", linewidth=2)

ax.set_xlabel('Time Steps')
ax.set_ylabel('Neural Activity (S)')
ax.set_title('Neural Activity Trajectories: Comparing Parameter Optimization Methods')
ax.legend(loc="right")
ax.grid(True, alpha=0.3)
ax.set_xlim(0, 1000)
plt.tight_layout()
plt.show()

This visualization shows how the different parameter optimization approaches perform in achieving the desired fixed point.