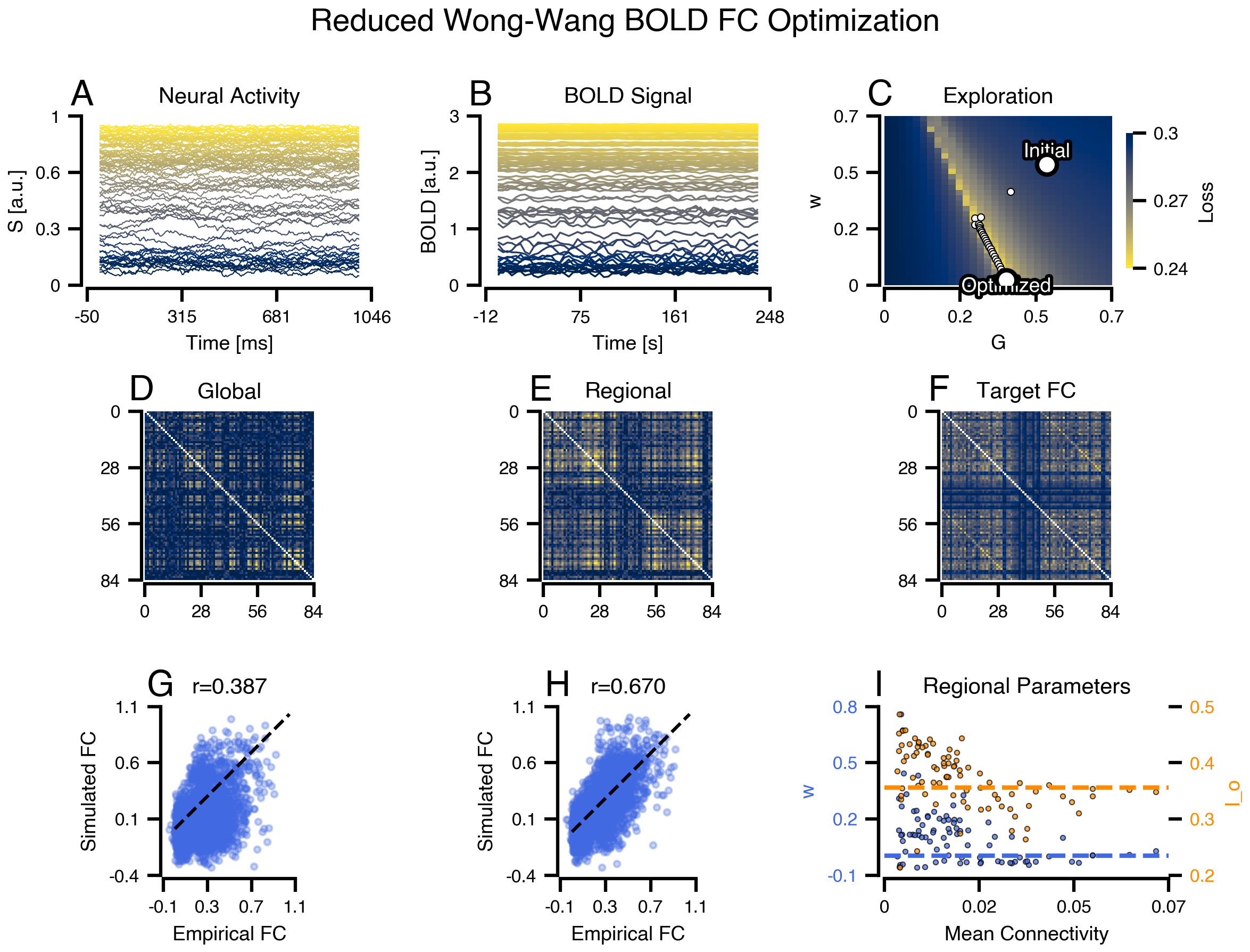
# | fig-cap: "**RWW BOLD FC Optimization.** (A) Neural activity. (B) BOLD signal. (C) Parameter landscape with trajectory. (D-F) FC matrices: target, global, regional. (G-H) FC scatter plots. (I-J) Fitted regional parameters."
import bsplot
from matplotlib.colors import Normalize
import matplotlib.pyplot as plt
import matplotlib.patheffects as path_effects
import jax.numpy as jnp
import numpy as np
from tvboptim.observations.observation import fc_corr
mosaic = """
AABBCC
DDEEFF
GGHHII
"""
fig, axes = plt.subplot_mosaic(mosaic, layout='tight', figsize=(8, 6))
cmap = plt.cm.cividis
fc_target = results.integration.main.observations.empirical_fc
# A: Neural Activity
ax = axes["A"]
t_max = int(1000 / exp.integration.step_size)
data = results.integration.main.data[:t_max, 0, :]
norm = Normalize(vmin=data.mean(0).min(), vmax=data.mean(0).max())
for i in range(data.shape[1]):
ax.plot(
results.integration.main.time[:t_max],
data[:, i],
color=cmap(norm(data.mean(0)[i])),
lw=0.5,
)
ax.set(xlabel="Time [ms]", ylabel="S [a.u.]", title="Neural Activity")
# B: BOLD Signal
ax = axes["B"]
bold = results.integration.main.observations.bold
data = bold.data[:60, 0, :]
norm = Normalize(vmin=data.mean(0).min(), vmax=data.mean(0).max())
for i in range(data.shape[1]):
ax.plot(bold.time[:60], data[:, i], color=cmap(norm(data.mean(0)[i])), lw=0.8)
ax.set(xlabel="Time [s]", ylabel="BOLD [a.u.]", title="BOLD Signal")
# C: Parameter Landscape with Trajectory
ax = axes["C"]
expl = results.exploration.parameter_landscape
pc = expl.grid.collect()
G_vals, w_vals = pc.coupling.FastLinearCoupling.G.flatten(), pc.dynamics.w.flatten()
im = ax.imshow(
jnp.stack(expl.results).reshape(32, 32).T,
cmap="cividis_r",
extent=[G_vals.min(), G_vals.max(), w_vals.min(), w_vals.max()],
origin="lower",
aspect="auto",
)
plt.colorbar(im, ax=ax, label="Loss", shrink=0.8)
# Initial & fitted points
for label, G, w, dy in [
(
"Initial",
results.state.coupling.FastLinearCoupling.G,
results.state.dynamics.w,
0.03,
),
(
"Optimized",
results.global_optimization.fitted_params.coupling.FastLinearCoupling.G.value,
results.global_optimization.fitted_params.dynamics.w.value,
-0.05,
),
]:
ax.scatter(
G, w, color="white", s=80, marker="o", edgecolors="k", linewidths=2, zorder=5
)
ax.annotate(
label,
(G, w),
xytext=(G, w + dy),
color="white",
fontweight="bold",
ha="center",
path_effects=[path_effects.withStroke(linewidth=3, foreground="black")],
)
# Trajectory
route = results.optimization.global_optimization.state_trajectory
ax.scatter(
[s.coupling.FastLinearCoupling.G.value for s in route],
[s.dynamics.w.value for s in route],
color="white",
s=10,
marker="o",
edgecolors="k",
linewidths=0.5,
zorder=4,
)
ax.set(xlabel="G", ylabel="w", title="Exploration")
# D-F: FC Matrices
for key, fc, title in [
("D", np.array(results.optimization.global_optimization.simulation.observations.fc), f"Global"),
("E", np.array(results.optimization.regional_optimization.simulation.observations.fc), f"Regional"),
("F", fc_target, "Target FC"),
]:
ax = axes[key]
fc_plot = np.copy(fc)
np.fill_diagonal(fc_plot, np.nan)
ax.imshow(fc_plot, cmap="cividis", vmin=0, vmax=0.9)
ax.set(xticks=[], yticks=[], title=title)
# G-H: Scatter Plots
triu = np.triu_indices_from(fc_target, k=1)
for key, fc, title in [
("G", results.optimization.global_optimization.simulation.observations.fc, "Global Fit"),
("H", results.optimization.regional_optimization.simulation.observations.fc, "Regional Fit"),
]:
ax = axes[key]
ax.scatter(fc_target[triu], np.array(fc)[triu], alpha=0.3, s=8, color="royalblue")
ax.plot([0, 1], [0, 1], "k--", lw=1.5)
ax.set(
xlabel="Empirical FC",
ylabel="Simulated FC",
title=f"r={fc_corr(fc, fc_target):.3f}",
aspect="equal",
)
# I: Fitted Regional Parameters (dual y-axis)
mean_conn = exp.network.weights.mean(axis=1)
opt_g, opt_r = results.global_optimization, results.regional_optimization
ax1 = axes["I"]
ax2 = ax1.twinx()
# Left axis: w (blue)
ax1.scatter(
mean_conn,
opt_r.fitted_params.dynamics.w.value.flatten(),
alpha=0.7,
s=5,
color="royalblue",
edgecolors="k",
lw=0.5,
label="w (regional)",
)
ax1.axhline(
opt_g.fitted_params.dynamics.w.value,
color="royalblue",
ls="--",
lw=2,
label=f"w (global): {float(opt_g.fitted_params.dynamics.w.value):.3f}",
)
ax1.set_xlabel("Mean Connectivity")
ax1.set_ylabel("w", color="royalblue")
ax1.tick_params(axis="y", labelcolor="royalblue")
# Right axis: I_o (orange)
ax2.scatter(
mean_conn,
opt_r.fitted_params.dynamics.I_o.value.flatten(),
alpha=0.7,
s=5,
color="darkorange",
edgecolors="k",
lw=0.5,
label="I_o (regional)",
)
ax2.axhline(
opt_g.fitted_params.dynamics.I_o,
color="darkorange",
ls="--",
lw=2,
label=f"I_o (global): {float(opt_g.fitted_params.dynamics.I_o):.3f}",
)
ax2.set_ylabel("I_o", color="darkorange")
ax2.tick_params(axis="y", labelcolor="darkorange")
ax1.set_title("Regional Parameters")
# lines1, labels1 = ax1.get_legend_handles_labels()
# lines2, labels2 = ax2.get_legend_handles_labels()
# ax1.legend(lines1 + lines2, labels1 + labels2, loc="upper right", fontsize=8)
plt.suptitle(
"Reduced Wong-Wang BOLD FC Optimization", fontsize=14, fontweight="bold", y=1
)
bsplot.style.format_fig(fig)
##